12)

Eine informelle Definition:

Definition: Halbgerade $AB^+$

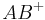Gegeben seien zwei verschiedene Punkte $\ A$ und $\ B$. Unter dem Strahl bzw. der Halbgeraden $\ AB^+$ versteht man die Strecke $\overline{AB}$ vereinigt mit der Menge aller der Punkte, die man erhält, wenn man $\overline{AB}$ über $\ B$ hinaus verlängert.

Formulieren Sie eine mathematisch korrekte Definition des Begriffs Halbgerade 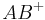$\ AB^+$.

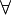Es seien A und B zwei verschiedene Punkte. Die Halbgerade $AB^+$ ist die Strecke $\overline{AB}$ vereinigt mit der Punktmenge aller Punkte P, für die gilt: $\forall$ P : $\operatorname(Zw) (A, B, P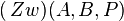)$ --Teufelchen777 01:02, 25. Nov. 2011 (CET)

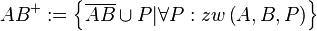$\ AB^{+} :=\left\{ {\overline{AB} \cup P|\forall P:zw\left( A,B,P\right) } \right\}$ --RicRic 12:40, 4. Dez. 2011 (CET)