12)
Aus Geometrie-Wiki
Version vom 5. Dezember 2011, 20:15 Uhr von Miriam (Diskussion | Beiträge)
Beweisen Sie: Zu jeder Strecke  existiert genau eine Strecke
existiert genau eine Strecke  mit
mit  und
und  .
.
Vor.: Es sei  eine Strecke.
eine Strecke.
Beh.: 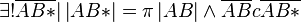
Bew.:Existenz:
| Schritt | Begründung |
|---|---|
(2) 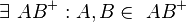 |
Def Strahl |
(3) 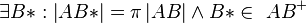 |
A vom Lineal, (2) |
(4) 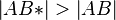 |
(3),da Abstand 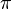 mal so groß mal so groß
|
(5) 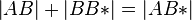 |
zw. Relation, (4),(3) |
| (6) zw(A,B,B*) | (5) |
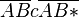 |
(6),(2),(3) |
Ein schöner Beweis.
zu Schritt 5, Begründung: Kann ich nicht ganz nachvollziehen - steht das in der Definition Zwischenrelation?--Tutorin Anne 17:29, 4. Dez. 2011 (CET)
zu Schritt 6 - Jetzt folgerst du daraus die Zwischenrelation, nutz sie vorher (5) aber schon zur Begründung -mh?--Tutorin Anne 17:29, 4. Dez. 2011 (CET)
- könnte man schritt 5 nicht so belassen und als begründung einfach anführen, dass die punkte kollinear sind und dementsprechend die dreiecksungleichung anführen?--Miriam 20:15, 5. Dez. 2011 (CET)
Bew.:Eindeutigkeit:
Ann.: 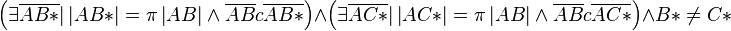
| Schritt | Begründung |
|---|---|
(1) 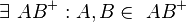 |
Def Strahl |
(2) 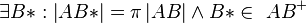 |
A vom Lineal, (1) |
(3) 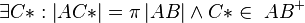 |
A vom Lineal, (1) |
(4) 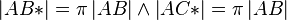 |
(2),(3) |
(5) 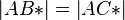 |
Rechen in R, (4) |
(6) 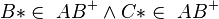 |
(2),(3) |
| (7)Fehler beim Parsen(Unbekannte Funktion „\lightning“): B* = C* \lightning zur Ann. ,diese ist zu Verwerfen | A vom Lineal (6),(4)--RicRic 13:32, 4. Dez. 2011 (CET) |

