Übung Aufgaben 6 (SoSe 12): Unterschied zwischen den Versionen

Aus Geometrie-Wiki
Wechseln zu: Navigation, Suche
 
(3 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt)
Zeile 1: Zeile 1:
−
= Aufgabe zur Inzidenz =
+
= Aufgaben zum Abstand und zur Anordnung =
−
=== Aufgabe 6.1 ===
+
== Aufgabe 6.1 ==
  
−
Es sei <math>\ g</math> eine Gerade und <math>\ P</math> ein Punkt, der nicht zu <math>\ g</math> gehört. Beweisen Sie mittels der Axiome der Inzidenz: Es gibt genau eine Ebene <math>\ \epsilon</math>, die sowohl alle Punkte von <math>\ g</math> als auch den Punkt <math>\ P</math> enthält.<br />
+
Definieren Sie: Strecke, Länge einer Strecke, die Halbgerade <math>AB^+</math> und die Halbgerade <math>AB^-</math>. Suchen Sie verschiedene Schreibweisen. (Hilfe finden Sie im Skript "Abstand, Anordnung, Strecke".)<br />
  
−
[[Lösung von Aufgabe 6.1 (SoSe_12)]]
+
[[Lösung von Aufgabe 6.1_S (SoSe_12)]]
  
−
= Aufgaben zum Abstand und zur Anordnung =
+
== Aufgabe 6.2 ==
  
 +
Warum ist die folgende Aufgabenstellung sinnlos?<br />
 +
Beweisen Sie Axiom II.2: Für beliebige Punkte <math>A</math> und <math>B</math> gilt: <math>\left| AB \right| </math> =  <math>\left| BA \right| </math><br />
 +
[[Lösung von Aufgabe 6.2_S (SoSe_12)]]
 +
 +
== Aufgabe 6.3 ==
 +
Beweisen Sie: Jede Strecke hat höchstens einen Mittelpunkt.<br />
 +
[[Lösung von Aufgabe 6.3_S (SoSe_12)]]
 +
<br />
 
==Aufgabe 5.2==
 
==Aufgabe 5.2==
 +
Diese Aufgabe war letzte Woche noch zu schwer- sorry dafür. Versuchen Sie es diese Woche nochmal.<br />
 
Zeigen Sie, dass für drei paarweise verschiedene Punkte <math>\ A, B</math> und <math>\ C</math> gilt:<br />
 
Zeigen Sie, dass für drei paarweise verschiedene Punkte <math>\ A, B</math> und <math>\ C</math> gilt:<br />
 
<math>\operatorname Zw (A, B, C) </math> <math>\Rightarrow </math> <math>\overline{AB} </math> <math> \subset</math>  <math>\overline{AC} </math>
 
<math>\operatorname Zw (A, B, C) </math> <math>\Rightarrow </math> <math>\overline{AB} </math> <math> \subset</math>  <math>\overline{AC} </math>
Zeile 17: Zeile 26:
  
 
==Aufgabe 5.4==
 
==Aufgabe 5.4==
 +
Wie bei 5.2: Versuchen Sie es diese Woche nochmal.<br />
 
Beweisen Sie: Zu jeder Strecke <math>\overline{AB} </math> existiert genau eine Strecke <math>\overline{AC} </math> auf <math>\ AB^{+} </math> mit <math>\left| AB \right| = \frac{1}{4} \left| AC \right| </math> und <math>\overline{AB} </math> <math> \subset</math>  <math>\overline{AC} </math>
 
Beweisen Sie: Zu jeder Strecke <math>\overline{AB} </math> existiert genau eine Strecke <math>\overline{AC} </math> auf <math>\ AB^{+} </math> mit <math>\left| AB \right| = \frac{1}{4} \left| AC \right| </math> und <math>\overline{AB} </math> <math> \subset</math>  <math>\overline{AC} </math>
 
<br />
 
<br />
Zeile 22: Zeile 32:
 
<br /><br />
 
<br /><br />
 
[[Lösung von Aufgabe 5.4 (SoSe_12)]]
 
[[Lösung von Aufgabe 5.4 (SoSe_12)]]
−
 
−
=== Aufgabe 6.1 ===
 
−
 
−
Definieren Sie: Strecke, Länge einer Strecke, die Halbgerade <math>AB^+</math> und die Halbgerade <math>AB^-</math>. Suchen Sie verschiedene Schreibweisen. (Hilfe finden Sie im Skript "Abstand, Anordnung, Strecke".)
 
−
 
−
[[Lösung von Aufgabe 6.1 (SoSe_12)]]
 
−
 
−
=== Aufgabe 6.1 ===
 
−
 
−
a) Definieren Sie windschief auf der Menge aller Geraden (d.h.im Raum) auf zwei verschiedene Arten. <br />
 
−
b) Warum ist die folgende Definition sinnlos?<br />
 
−
::Zwei Ebenen sind windschief, wenn sie sich nicht schneiden und sie nicht parallel zueinander sind.<br />
 
−
 
−
[[Lösung von Aufgabe 6.1 (SoSe_12)]]
 
−
 
−
 
−
=== Aufgabe 6.1 ===
 
−
 
−
Im Skript steht als Beweis "trivial". Führen Sie die Beweise trotzdem mal durch. Gehen Sie kleinschrittig und gut begründet vor.<br />
 
−
Beweisen Sie:<br />
 
−
a) <math>\operatorname Zw (A, B, C) </math> <math>\Rightarrow </math>  <math>\operatorname Zw (C, B, A) </math><br />
 
−
b) <math>\operatorname Zw (A, B, C) </math> <math>\Rightarrow </math>  <math>\operatorname koll (A, B, C) </math><br />
 
−
 
−
[[Lösung von Aufgabe 6.1 (SoSe_12)]]
 
−
 
−
=== Aufgabe 6.1 ===
 
−
 
−
Warum ist die folgende Aufgabenstellung sinnlos?<br />
 
−
Beweisen Sie Axiom II.2: Für beliebige Punkte <math>A</math> und <math>B</math> gilt: <math>\left| AB \right| </math> =  <math>\left| BA \right| </math><br />
 
−
[[Lösung von Aufgabe 6.1 (SoSe_12)]]
 
−
 
−
=== Aufgabe 6.1 ===
 
−
== Aufgabe 9.1 ==
 
−
Es seien A und B zwei verschiedene Punkte. Welche Ergebnisse erzielen Sie nach den folgenden Mengenoperationen?
 
−
 
−
a) <math>\ AB^{+} \cap BA^{+} =</math> <br\>
 
−
 
−
b) <math>\ AB^{-} \cap BA^{-} =</math> <br\>
 
−
 
−
c) <math>\ AB </math> geschnitten mit dem Kreis um <math>\ A </math> durch <math>\ B </math> =
 
−
 
−
d)<math>\ AB \cap BA =</math> <br\>
 
−
 
−
 
−
[[Lösung von Aufgabe 6.1 (SoSe_12)]]
 

Aktuelle Version vom 22. Mai 2012, 22:01 Uhr

Inhaltsverzeichnis

Aufgaben zum Abstand und zur Anordnung

Aufgabe 6.1

Definieren Sie: Strecke, Länge einer Strecke, die Halbgerade AB^+ und die Halbgerade AB^-. Suchen Sie verschiedene Schreibweisen. (Hilfe finden Sie im Skript "Abstand, Anordnung, Strecke".)

Lösung von Aufgabe 6.1_S (SoSe_12)

Aufgabe 6.2

Warum ist die folgende Aufgabenstellung sinnlos?
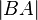
Beweisen Sie Axiom II.2: Für beliebige Punkte A und B gilt: \left| AB \right| = \left| BA \right|
Lösung von Aufgabe 6.2_S (SoSe_12)

Aufgabe 6.3

Beweisen Sie: Jede Strecke hat höchstens einen Mittelpunkt.
Lösung von Aufgabe 6.3_S (SoSe_12)

Aufgabe 5.2

Diese Aufgabe war letzte Woche noch zu schwer- sorry dafür. Versuchen Sie es diese Woche nochmal.
Zeigen Sie, dass für drei paarweise verschiedene Punkte \ A, B und \ C gilt:
\operatorname Zw (A, B, C) \Rightarrow \overline{AB} \subset \overline{AC}

Tipps zu Aufgabe 5.2 (SoSe_12)

Lösung von Aufgabe 5.2 (SoSe_12)

Aufgabe 5.4

Wie bei 5.2: Versuchen Sie es diese Woche nochmal.
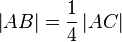Beweisen Sie: Zu jeder Strecke \overline{AB} existiert genau eine Strecke \overline{AC} auf \ AB^{+} mit \left| AB \right| = \frac{1}{4} \left| AC \right| und \overline{AB} \subset \overline{AC}
Tipps zu Aufgabe 5.4 (SoSe_12)

Lösung von Aufgabe 5.4 (SoSe_12)

Von „http://geometrie.zum.de/index.php?title=Übung_Aufgaben_6_(SoSe_12)&oldid=13730“