Übung Aufgaben 6 (SoSe 12)
Inhaltsverzeichnis |
Aufgaben zum Abstand und zur Anordnung
Aufgabe 6.1
Definieren Sie: Strecke, Länge einer Strecke, die Halbgerade  und die Halbgerade
und die Halbgerade  . Suchen Sie verschiedene Schreibweisen. (Hilfe finden Sie im Skript "Abstand, Anordnung, Strecke".)
. Suchen Sie verschiedene Schreibweisen. (Hilfe finden Sie im Skript "Abstand, Anordnung, Strecke".)
Lösung von Aufgabe 6.1_S (SoSe_12)
Aufgabe 6.2
Warum ist die folgende Aufgabenstellung sinnlos?
Beweisen Sie Axiom II.2: Für beliebige Punkte  und
und  gilt:
gilt:  =
= 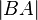
Lösung von Aufgabe 6.2_S (SoSe_12)
Aufgabe 6.3
Beweisen Sie: Jede Strecke hat höchstens einen Mittelpunkt.
Lösung von Aufgabe 6.3_S (SoSe_12)
Aufgabe 5.2
Diese Aufgabe war letzte Woche noch zu schwer- sorry dafür. Versuchen Sie es diese Woche nochmal.
Zeigen Sie, dass für drei paarweise verschiedene Punkte  und
und  gilt:
gilt:





Tipps zu Aufgabe 5.2 (SoSe_12)
Lösung von Aufgabe 5.2 (SoSe_12)
Aufgabe 5.4
Wie bei 5.2: Versuchen Sie es diese Woche nochmal.
Beweisen Sie: Zu jeder Strecke  existiert genau eine Strecke
existiert genau eine Strecke  auf
auf  mit
mit 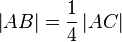 und
und 


Tipps zu Aufgabe 5.4 (SoSe_12)
Lösung von Aufgabe 5.4 (SoSe_12)

