Lösung von Aufg. 8.5 (WS 11/12): Unterschied zwischen den Versionen

Aktuelle Version vom 14. Dezember 2011, 19:02 Uhr

Beweisen Sie: Der Durchschnitt zweier konvexer Punktmengen ist konvex.

Eine Punktmenge ist konvex, wenn für alle Punkte A und B der Punktmenge gilt, dass alle Punkte von Element der Punktmenge P sind.

Vor: Es sind X und Y zwei konvexe Punktmengen.

Beh: 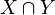ist Konvex
1. Es seien A und B zwei Punkte aus der Schnittmenge von X und Y ( Vor.)

2. 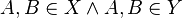und die Schnittmenge ist nicht leer ( Vor.)

3. 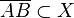und 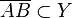(aus 2, Vor., Def. konvexe Punktmenge)

4. 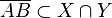( 3, Def. Schnittmenge)

5. 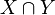ist eine konvexe Menge (4, Def. konvexe Menge ) --Costa rica 23:46, 5. Dez. 2011 (CET)

Woher weißt du dann, dass es zwischen den Punkten A und B auf der Strecke es nicht noch irgendeinen Punkt P gibt, der nicht in beiden Teilmengen ist?
Finde den Beweis Übrigens gut und nachvollziehbar, bin mir aber nicht sicher ob er ausreicht. --RicRic 17:15, 6. Dez. 2011 (CET)

Also, X und Y sind je zwei konvexe Punktmengen. Zwei beliebige Punkte A und B liegen in X und in Y. Nach Def. konvex liegt dann auch die gesamte strecke AB in X. Das gleiche gilt für Y. Folglich ist die Schnittmenge X Y auch konvex. (Def. konvexe Punktmenge)--Costa rica 00:37, 9. Dez. 2011 (CET)

Ich habe in dem Beweis die korekte Formelschreibweise eingefügt, damit dieser besser verständlich ist. Die Beschreibung von Costa rica hilf sonst auch weiter - danke!
So kann man diesen Satz direkt beweisen. Allerdings geht der Beweis bestimmt auch indirekt, in dem man die Idee von RicRic verfolgt und einen Punkt P annimmt, der auf liegt und nicht in der Schnittmenge von X und Y enthalten ist.
Hier ist genug Platz, auch diesen Beweis zu führen - wer möchte sich versuchen?--Tutorin Anne 13:53, 14. Dez. 2011 (CET)