Lösung von Aufgabe 4.3 S (SoSe 12): Unterschied zwischen den Versionen

Aus Geometrie-Wiki
Wechseln zu: Navigation, Suche
(→‎Lösungsvorschlag 2 (Nemo81))
(→‎Teilaufgabe 2)
Zeile 38: Zeile 38:
 
|}
 
|}
  
 +
#Wie sieht es aus, wenn alle drei Punkte identisch sind, also A = B = C?--[[Benutzer:Andreas|Tutor Andreas]] 18:15, 22. Mai 2012 (CEST)
  
 
===Teilaufgabe 3===
 
===Teilaufgabe 3===

Version vom 22. Mai 2012, 18:15 Uhr

Inhaltsverzeichnis

Aufgabe 4.3

Satz I: Je drei nicht kollineare Punkte sind paarweise verschieden.

  1. Wir formulieren Satz I neu und beginnen mit „Es seien A, B und C drei Punkte.“ Ergänzen Sie: „Wenn A,B und C … , dann … .“
  2. Beweisen Sie Satz I indirekt mit Widerspruch.
  3. Bilden Sie die Kontraposition von Satz I.
  4. Beweisen Sie auch die Kontraposition von Satz I.
  5. Formulieren Sie die Umkehrung von Satz I.
  6. Gilt auch die Umkehrung von Satz I?



Lösungsvorschlag 1 (Numero6)

Teilaufgabe 1

„Wenn A,B und C nicht kollinear sind, dann sind sie paarweise verschieden.“

Teilaufgabe 2


Voraussetzung: nkoll (A,B,C)
Behauptung: A,B und C sind paarweise verschieden
Annahme: 2 Punkte sind nicht paarweise verschieden (Widerspruch zur Behauptung..)

Beweisschritt Begründung
(1) 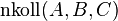\operatorname{nkoll}(A, B, C) Voraussetzung
(2) oBdA: 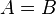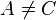A=B ; A \neq C Annahme
(3) 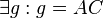\exists g:g=AC (2), Axiom I/1
(4) 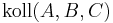\operatorname{koll}(A, B, C) (2), (3), Def. kollinear
(5) Widerspruch zur Voraussetzung (4), (1)
(6) Behauptung stimmt (5)
  1. Wie sieht es aus, wenn alle drei Punkte identisch sind, also A = B = C?--Tutor Andreas 18:15, 22. Mai 2012 (CEST)

Teilaufgabe 3

„Wenn A,B und C nicht paarweise verschieden sind, dann sind sie kollinear.“

Teilaufgabe 4


Voraussetzung: mindestens 2 der 3 Punkte (A,B,C) sind identisch
Behauptung: koll (A,B,C)

Beweisschritt Begründung
(1) oBdA: 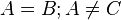A=B ; A \neq C Voraussetzung
(2) 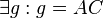\exists g:g=AC (1), Axiom I/1
(3) 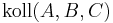\operatorname{koll}(A, B, C) (1), (2), Def. kollinear


Teilaufgabe 5

„Wenn A,B und C paarweise verschieden sind, dann sind sie nicht kollinear.“

Teilaufgabe 6

Die Umkehrung von Satz I gilt NICHT!!! (siehe Gegenbeispiel)


--Tchu Tcha Tcha 19:12, 13. Mai 2012 (CEST)

Lösungsvorschlag 2 (Nemo81)

Hier mal meine Lösung, glaube dass die nicht wirklich gut ist.

@Nemo81 Es gibt nichts Gutes, außer man tut es. --*m.g.* 19:05, 19. Mai 2012 (CEST) Ich hab Ihre Ausführungen hier nur mal wegen der besseren Übersichlichkeit in ein Tabelle eingetragen. Jetzt starte ich mal auf der Hauptseite einen Aufruf, Ihnen zu helfen.

Vor: A,B,C nkoll
Beh: A,B,C paarweise verschieden


Ann: Fall 1 A=B=C


Nr. Beweisschritt Begründung
1) A,B,C nkoll laut Vor
2) Es gibt eine Menge von Geraden AB,AC,BC laut Axiom I/1 und 1)
3) A=B=C laut Ann
4) Es exsistiert eine Gerade g mit A,B,C Element von g Def I/2 Kollinear und 3)
5) Widerspruch zur Behauptung laut 1) und 2) gibt es Eine Menge von Geraden die AB,AC,BC und laut 3) und 4) sollen die Punkte A,B,C auf einer Geraden g liegen.


--Nemo81 14:22, 19. Mai 2012 (CEST)

Von „http://geometrie.zum.de/index.php?title=Lösung_von_Aufgabe_4.3_S_(SoSe_12)&oldid=13702“