Serie 5 (WS 12 13): Unterschied zwischen den Versionen

Aus Geometrie-Wiki
Wechseln zu: Navigation, Suche
(→‎Aufgaben zum Abstand)
(→‎Aufgabe 5.2)
Zeile 9: Zeile 9:
  
 
==Aufgabe 5.2==
 
==Aufgabe 5.2==
−
Es seien <math>A</math>, <math>B</math>, <math>C</math> und <math>D</math> vier paarweise verschiedene Punkte. <br />  
+
Gegeben seien eine rote Kugel aus Knete (R), eine blaue Kugel aus Knete (B), eine grüne Kugel aus Knete (G) und eine schwarze Kugel aus Knete (K). Aus einem Mikadospiel wurde jeweils genau ein Repräsentant der folgenden Stäbchenart entnommen: Mikado, Mandarin, Bonzen und Samurai.<br />
−
Beweisen Sie:<br />
+
Wir betrachten das folgende Modell für die Inzidenz:<br />
−
<math>\overline{CD} \subset \overline{AB} \Rightarrow \forall P \in \overline{CD}: \operatorname{Zw}(APB}</math>.
+
*Menge aller Punkte <math>\mathbb{P}:=\{R. G, B, K\}</math>
 +
*Menge aller Geraden <math>\mathbb{G}:=\{Mikado, Mandarin, Bonzen, Samurei\}</math>
  
  

Version vom 24. November 2012, 14:49 Uhr

Inhaltsverzeichnis

weitere Aufgaben zur Inzidenz

Aufgabe 5.1

Begründen Sie:

  1. Jedes Modell für die Inzidenzaxiome der Ebene beinhaltet wenigstens 3 paarweise verschiedene Punkte.
  2. Jedes Modell für die Inzidenzaxiome des Raumes beinhaltet wenigstens 3 paarweise verschiedene Punkte.


Lösung von Aufgabe 5.1_S (WS_12_13)

Aufgabe 5.2

Gegeben seien eine rote Kugel aus Knete (R), eine blaue Kugel aus Knete (B), eine grüne Kugel aus Knete (G) und eine schwarze Kugel aus Knete (K). Aus einem Mikadospiel wurde jeweils genau ein Repräsentant der folgenden Stäbchenart entnommen: Mikado, Mandarin, Bonzen und Samurai.
Wir betrachten das folgende Modell für die Inzidenz:

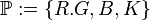
  • Menge aller Punkte \mathbb{P}:=\{R. G, B, K\}
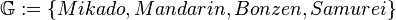
  • Menge aller Geraden \mathbb{G}:=\{Mikado, Mandarin, Bonzen, Samurei\}




Lösung von Aufgabe 5.2_S (WS_12_13)

Aufgabe 5.3

Zeigen Sie, dass für drei paarweise verschiedene Punkte \ A, B und \ C gilt:
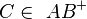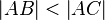Wenn C \in \ AB^{+} und \left| AB \right| < \left| AC \right| dann gilt \operatorname Zw (A, B, C)


Lösung von Aufgabe 5.3_S (WS_12_13)


Aufgabe 5.4

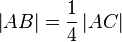Beweisen Sie: Zu jeder Strecke \overline{AB} existiert genau eine Strecke \overline{AC} auf \ AB^{+} mit \left| AB \right| = \frac{1}{4} \left| AC \right| und \overline{AB} \subset \overline{AC}



Lösung von Aufgabe 5.4_S (WS_12_13)

Weitere Aufgabe zur Inzidenz

Aufgabe 5.5

Beweisen Sie: Je vier nicht komplanare Punkte sind paarweise verschieden (Hinweis: Nutzen Sie bei der Beweisführung die Sätze aus Aufgabe 4.3 und Zusatzaufgabe 4.4).

Lösung von Aufg. 5.5_S (WS_12_13)

Von „http://geometrie.zum.de/index.php?title=Serie_5_(WS_12_13)&oldid=18925“