Übung Aufgaben 9 (WS 11/12)
Inhaltsverzeichnis[Verbergen] |
Aufgabe 9.1
Es seien A und B zwei verschiedene Punkte. Welche Ergebnisse erzielen Sie nach den folgenden Mengenoperationen?
a) 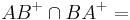
b) 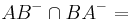
c)  geschnitten mit dem Kreis um
geschnitten mit dem Kreis um  durch
durch  =
=
d)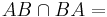
Lösung von Aufg. 9.1 (WS_11/12)
Aufgabe 9.2
Definieren Sie den Begriff Strahl  . Verwenden Sie dabei den Begriff Strecke.
. Verwenden Sie dabei den Begriff Strecke.
Lösung von Aufg. 9.2 (WS_11/12)
Aufgabe 9.3
Definition (gemeiner Dreiecksschneider): Unter einem gemeinen Dreieckschneider versteht man eine Gerade, die alle drei offenen Seiten eines Dreiecks schneidet.
Beschreiben Sie die Menge aller gemeinen Dreiecksschneider und begründen Sie Ihre Aussage.
Lösung von Aufg. 9.3 (WS_11/12)
Aufgabe 9.4
Gegeben seien drei paarweise verschiedene und kollineare Punkte A, B und C in einer Ebene E. Ferner sei eine Gerade g Teilmenge der Ebene E, wobei keiner der Punkte A, B und C auf g liegen möge. Beweisen Sie folgenden Zusammenhang:
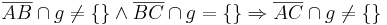
Lösung von Aufg. 9.4 (WS_11/12)
Aufgabe 9.5
a) Definieren Sie den Begriff: "Konkave Punktmenge" ohne den Begriff "konvex" zu gebrauchen.
b) Begründen Sie, dass der Schnitt einer offenen Halbebene E mit einer Halbgeraden, die zwei Punkte mit E gemeinsam hat, auf jeden Fall eine konvexe Punktmenge ist.
c) Zeigen Sie an einem Beispiel, dass die Vereinigungsmenge des Inneren zweier Drachenvierecke, die keine Rauten sind, konkav sein kann.
Lösung von Aufg. 9.5 (WS_11/12)
Aufgabe 9.6
Unter dem Raum 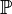 versteht man die Menge aller Punkte. Die Punktmenge
versteht man die Menge aller Punkte. Die Punktmenge
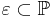 sei eine Ebene. Gegeben sei ferner
sei eine Ebene. Gegeben sei ferner  mit
mit 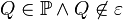 . Definieren Sie die Begriffe Halbraum
. Definieren Sie die Begriffe Halbraum 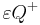 und
und 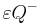 .
Lösung von Aufg. 9.6 (WS_11/12)
.
Lösung von Aufg. 9.6 (WS_11/12)

