Bin ich für die Klausur fit Teil 2? SS12

Testaufgabe 2.1 (Definieren)

Definieren Sie den Begriff Viereck, ohne den Oberbegriff n-Eck zu verwenden.
Hilfe:

Sie benötigen die Begriffe komplanar und kollinear. Sie kennen schon die Definition eines analogen einfacheren Begriffes.

Testbedingungen:

Kein Nachschlagen, kein gemeinschaftliches Arbeiten nur aus der Kraft der eigenen Überlegungen, 5 Minuten

Lösung von Testaufgabe 2.1 SS12

Testaufgabe 2.2 (Definieren)

Definieren Sie: Die Gerade $s$ ist eine Sekante bzgl. des Kreises $k$.
Bemerkung:

Den Begriff Sekante haben wir nirgends geklärt. So viel Schulwissen sollte jedoch sein.

(lateinisch: secare = „schneiden“)

Zeit:

1 Minute

Lösung von Testaufgabe 2.2 SS12

Testaufgabe 2.3 (Beweisen, Anordnung, Abstand)

Beweisen Sie: Wenn ein von den Punkten $A$ und $B$ verschiedener Punkt $P$ zur Halbgeraden $AB^+$ gehört, dann gehört er nicht zur Halbgeraden $AB^-$.
Bemerkungen:

Sie sollten ad hoc wissen, worauf der Beweis hinausläuft.

Zeit:

1 Minute

Lösung von Testaufgabe 2.3 SS12

Testaufgabe 2.4 (Beweisen mit einer Umkehrung)

Der Satz des Thales lautet:

Wenn der Scheitelpunkt des Winkels 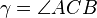$\gamma=\angle ACB$ auf dem Keis $k$ mit dem Durchmesser $\overline{AB}$ liegt, dann ist $\gamma$ ein rechter Winkel.

Im Folgenden dürfen Sie davon ausgehen, dass der Satz des Thales bereits bewiesen wurde.

Beweisen Sie:

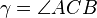Es sei $\overline{AB}$ ein Durchmesser des Kreises $k$. Wenn der Punkt $C$ im Inneren von $k$ liegt, dann ist der Winkel $\gamma=\angle ACB$ kein rechter Winkel.

Hilfe:

Skizze anfertigen, zur Tahlessatzfigur ergänzen. Formulierung des Beweises mit starkem Bezug zur Skizze.

Zeit:

max 20 Minuten

Lösung von Testaufgabe 2.4 SS12

Testaufgabe 2.5 (grundlegende Kenntnisse zur Aussagenlogik)

Es sei $\overline{AB}$ ein Durchmesser des Kreises $k$.

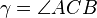Formulieren Sie die Kontraposition der folgenden Implikation: Wenn der Punkt $C$ im Inneren von $k$ liegt, dann ist der Winkel $\gamma=\angle ACB$ kein rechter Winkel.

Zeit:

30 Sekunden

Lösung von Testaufgabe 2.5 SS12

Testaufgabe 2.6 (geometrisches Verständnis, Transfer)

Wir definieren den Begriff Tangentenviereck wie folgt:

Definition

---

(Tangentenviereck)
Wenn die Summe der Längen der gegenüberliegenden Seiten eines Vierecks gleich ist, dann ist dieses Viereck ein Tangentenviereck.

Satz D:

Jeder Drachen ist ein Tangentenviereck.

Aufgabe:

Geben Sie eine Definition des Begriffs Drachen an, mittels derer es möglichst einfach ist, Satz D zu beweisen. Beweisen Sie dann Satz D.

Zeit: 10 Minuten

Lösung von Testaufgabe 2.6 SS12