Das Lot von einem Punkt auf eine Gerade WS 11/12
Aus Geometrie-Wiki
Inhaltsverzeichnis |
Der Begriff des Lotes
Definition IX.1: (Lot, Lotgerade, Lotfußpunkt)
- Es sei
 ein Punkt, der nicht zur Geraden
ein Punkt, der nicht zur Geraden  gehören möge. Ferner sei
gehören möge. Ferner sei  ein Punkt der zu
ein Punkt der zu  gehören möge.
gehören möge.
- Die Strecke
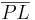 ist dann das Lot von
ist dann das Lot von  auf
auf  , wenn
, wenn 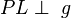
-
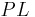 ist die Lotgerade und
ist die Lotgerade und  der Lotfußpunkt.--RicRic 20:31, 5. Jan. 2012 (CET)
der Lotfußpunkt.--RicRic 20:31, 5. Jan. 2012 (CET)
- Es sei
Ihre Definition ist prinzipiell OK, ich würde allerdings empfehlen die sachlogische Reihenfolge zu beachten, d. h. wir definieren erst die Lotgerade
l als Senkrechte auf g durch P, dann den Lotfußpunkt L als Schnittpunkt von l und g und dann das Lot als Strecke.--Schnirch 13:20, 17. Jan. 2012 (CET)
Definition IX.2: (Abstand eines Punktes zu einer Geraden)
- Es sei
 ein Punkt außerhalb von
ein Punkt außerhalb von  . Der Abstand von
. Der Abstand von  zu
zu  ist die Länge des Lotes von
ist die Länge des Lotes von  auf
auf  . --*m.g.* 10:28, 6. Feb. 2012 (CET)--
. --*m.g.* 10:28, 6. Feb. 2012 (CET)--
- Es sei
Existenz und Eindeutigkeit des Lotes
Satz IX.1: (Existenz und Eindeutigkeit des Lotes)
- Zu jedem Punkt
 außerhalb einer Geraden
außerhalb einer Geraden  gibt es genau ein Lot von
gibt es genau ein Lot von  auf
auf  .
.
- Zu jedem Punkt
Beweis der Existenz und Eindeutigkeit des Lotes:
Übungsaufgabe

