Definition der Woche 13 (SoSe 11)

Die Semantik der folgenden Begriffe ist in der Begriffsbezeichnung jeweils enthalten:

1. Sehnenviereck
2. Tangentenviereck
3. Sehnen-Tangenten-Viereck

Definieren Sie diese drei Begriffe.

1. Gegeben sei ein Kreis k und ein Viereck $\overline{ABCD}$. $\overline{ABCD}$ ist ein Sehnenviereck, wenn A,B,C,D $\in$ k und nkoll(A,B,C,D) gilt.--Teufelchen 22:03, 6. Jul. 2011 (CEST)

Ich denke die Definition hat einen kleinen Haken. Nach deiner Definition wäre das hier kein Sehnenviereck:

Um es korrekt zu definieren, musst du vier Punkte (glaube ich) auf dem Kreis k plazieren:
Sei k ein Kreis und A, B, C, D vier paarweise verschiedene Punkte, für die gilt, dass sie Element von k sind.
Das Sehnenviereck: = 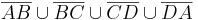$\overline{AB} \cup \overline{BC} \cup \overline{CD} \cup \overline{DA}$ --Flo60 23:10, 8. Jul. 2011 (CEST)

Ich denke, dass das Viereck in deiner Zeichnung kein Sehnenviereck ist, da keine Seite eine Sehne im Kreis darstellt. Somit behaupte ich, dass meine Def. richtig ist ;) --Teufelchen 14:59, 10. Jul. 2011 (CEST)

Ja doch auf jeden Fall, da ein Quadrat ein regelmäßiges n-Eck ist und dieses ist durch einen Umkreis definiert. Nur weil in der Zeichnung kein Umkreis erkennbar ist heißt das ja nicht, dass das Viereck keinen hat. Das ist dann so (und jetzt kommt der Megavergleich :-) ) wie wenn man sagt, dass in einem Wohnzimmer keine Stereoanlage steht, nur weil man grad keine Musik hören kann - sie ist aber da, halt nur nicht eingeschaltet. (Ich weiß der Vergleich ist dämlich und ich schäm mich fast ein wenig dafür :-) aber nur fast) --Flo60 20:54, 10. Jul. 2011 (CEST)

Angenommen, deine Zeichnung würde ein Sehnenviereck darstellen, wo sind dann die Sehnen? Ich denke immer noch, dass das keines ist. Aber eine Antwort eines Dozenten wäre gut, denn wir beide drehen uns im Kreis ;) --Teufelchen 02:11, 12. Jul. 2011 (CEST)

Hast recht, genaugenommen im (Um)Kreis :-)
--Flo60 09:04, 12. Jul. 2011 (CEST)
Ich sagen mal was dazu, obwohl ich kein Dozent bin :)
Ihr habt immer davon gesprochen, dass ein Viereck dann ein Sehnenviereck ist, wenn seine Eckpunkte auf einem gegebenen Kreis k liegen. Betrachten wir mal die Analogie zum Dreieck... dann wäre ein Dreieck ABC, dessen Eckpunkte nicht auf einem gegebenen Kreis k₁ liegen, kein "Sehnendreieck"... aber da jedes Dreieck einen Umkreis hat und die Eckpunkte somit auf einem Kreis liegen müssen, müssen die Seiten des Dreiecks ABC Sehnen eines Kreises k₂ sein... ist das Dreieck nun ein "Sehnendreieck" oder nicht? Ich hoffe das verwirrt nicht zu sehr..., ansonsten bitte gleich sagen, dann versuche ich anders zu helfen. --Tutor Andreas 17:23, 13. Jul. 2011 (CEST) Oder nochmal anders... zu jedem Dreieck ABC gibt es einen Umkreis, da durch 3 verschiedenen Punkten ein Kreis eindeutig bestimmt wird. Somit ist jedes Dreieck ein "Sehnendreieck" (diese Bezeichnung macht also keinen Sinn und man definiert diesen Begriff deshalb auch nicht).
Anders beim Sehnenviereck... Ein Viereck ist ein Sehnenviereck, wenn... (ergänzt hier mal und wir schauen dann mal weiter)--Tutor Andreas 11:37, 14. Jul. 2011 (CEST)

Folglich ist ein Sehnenviereck nur ein Viereck, dessen 4 Punkte auf dem Kreis liegen, richtig? Zur Frage: Das Dreieck ist ein Sehnendreieck. --Teufelchen 22:26, 13. Jul. 2011 (CEST)
Wenn du statt "dem Kreis" in deiner Aussage "einem Kreis" sagen würdest, dann würde ich eher zustimmen.--Tutor Andreas 11:37, 14. Jul. 2011 (CEST)

Liegt das daran, wenn ich "dem Kreis" schreibe, dann spreche ich von einem und nur von einem betimmten Kreis. Schreibe ich allerdings "ein Kreis", dann ist ein unbestimmter Kreis und somit viele Kreise gemeint. Richtig??--Teufelchen 20:30, 16. Jul. 2011 (CEST)

2. Ein Viereck mit einem Inkreis ist ein Tangentenviereck. --Teufelchen 22:03, 6. Jul. 2011 (CEST)

So hätte man das Sehnenviereck auch definieren können :-) Die Frage die bleibt ist aber glaube ich, was denn nun ein Innkreis ist?. Und darüber hinaus kann der Innkreis auch wieder kleiner sein und eben grad nicht tangieren.

Sei $\overline{ABCD}$ ein beliebiges Viereck. Wenn es einen Kreis k gibt, für den gilt, dass jede Seite des Vierecks den Kreis in jeweils genau einem Punkt schneidet, dann ist das Viereck ein Tangentenviereck.

AnmerkungWenn folgendes geschrieben hätte (und das habe ich vorher auch):
"Sei k ein Kreis und $\overline{ABCD}$ ein beliebiges Viereck. Wenn jede Seite des Vierecks den Kreis in jeweils genau einem Punkt schneidet, dann ist das Viereck ein Tangentenviereck."; dann wäre das Gleiche wie oben in der ersten Definition herausgekommen, d. h. nur weil Kreis k nicht tangiert heist dies noch nicht, dass das Viereck kein Tangentenviereck ist. In der vorherigen Definition schließen wir das aus, indem wir von vorneherein festlegen, "wenn es einen Kreis gibt" --Flo60 23:10, 8. Jul. 2011 (CEST)

Mit dem Inkreis gebe ich dir recht. Allerdings dachte ich, dass wir Inkreis bereits definiert hatten. Falls nicht: Ein Inkreis ist ein Kreis, der vollständig im Inneren eines Vierecks liegt und jede Seite in diesem Viereck berührt. Ich habe mehrfach schneidet gelesen, aber ich denke, das ist falsch, da es keinen Schnittpunkt sondern einen Berührpunkt gibt.
Zu deiner Anmerkung: Ich denke, dass auch diese Def richtig ist, wenn du schneidet durch berührt ersetzt. --Teufelchen 14:59, 10. Jul. 2011 (CEST)

3. Gibt es nicht, da ein Viereck entweder einen Inkreis, einen Umkreis oder nichts von beidem hat. --Teufelchen 22:03, 6. Jul. 2011 (CEST)

Was ist hiermit?--Tutor Andreas 23:56, 6. Jul. 2011 (CEST)

hmm, ok, das könnte sein. Aber gibt es sowas? Wäre diese Definition dann sinnvoll?
Ein Vierck ABCD ist ein Sehnen-Tangenten-Viereck, wenn 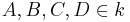$A,B,C,D \in k$ und das Viereck einen Inkreis hat.--Teufelchen 21:53, 8. Jul. 2011 (CEST)

Weil du die beiden Begriffe nun ja schon definiert hast, so kannst du dir das ganze nun einfacher machen, indem du sagst: Ein Viereck, das sowohl Tangenten, als auch Sehnenviereck ist, ist ein Sehnen-Tangenten-Viereck. --Flo60 23:19, 8. Jul. 2011 (CEST)

Hier wurde irgendwo mal gesagt, dass ein Berührpunkt kein Schnittpunkt ist... oder so. Nehmen wir mal an, dass ein Kreis k und eine Gerade g sich in einem Punkt P berühren. Dann muss P sowohl zu k als auch zu P gehören. Nach der Definition "Schnittmenge" liegt dieser Punkt dann auch in der Schnittmenge von k und g. Somit ist ein Berührpunkt auch ein Schnittpunkt. Ich denke, dass das nachvollziehbar ist. --Tutor Andreas 17:30, 13. Jul. 2011 (CEST)