Diskussion:Hauptseite SS10

In der Diskussionsecke können Sie beliebige Fragen, Probleme, Ideen, ... zur Geometrie einstellen. "Unterschreiben" Sie Ihre Beiträge am besten mit Ihrem Pseudonym, indem Sie "--~~~~" eingeben oder auf den "Signatur"-Button klicken:

Tragen Sie Ihre Frage bitte oben ein, sodass die neuesten Fragen immer ganz oben stehen Selbstverständlich können Sie auch hier Bilder, geometrische Konstruktionen etc. einbinden!

Allgeimein zu Geowiki

Ich habe ein Lösungsblatt für die Übungen 6 als pdf erstellt, weiß aber nicht wie ich es hochladen kann. Ich habe es schon als irgendetwas hochgeladen, aber ich weiß nicht wo es jetzt ist, bzw. weiß auch nicht wie ich es dann zu den Übungen stellen kann falls ich es weider "finde". Kann mir jemand helfen? Sorry, dass ich die Frage hier hin schreib, aber ich habe keine Diskussion zu allgemeinen Fragen gefunden.. --Bino37 09:38, 23. Jun. 2010 (UTC)

Geben Sie einfach den Dateinamen der hochgeladenen Datei z. B. folgendermaßen an: Lösungen zur Übungsserie 6 im pdf-Format--Schnirch 08:55, 24. Jun. 2010 (UTC)

Wie lernt man Mathematik?

Warum dreht man in den USA solche Serien wie Numbers. Natürlich wird in dieser Serie eine Menge mathematischer Blödsinn verzapft. Aber für eine Idee, dass Mathematik ziemlich sexy sein kann, würde man in Deutschland wohl ausgelacht werden. --*m.g.* 13:56, 21. Jun. 2010 (UTC)--*m.g.* 13:56, 21. Jun. 2010 (UTC)

Satz I.4

Hat jemand eine Ahnung wie der Satz I/4 lautet?

[1]--*m.g.* 11:30, 31. Mai 2010 (UTC)

Definitionen - sind sie richtig?

Parallelogramm: Ein Trapez mit einem weiteren Paar gegenüberliegender zueinander parallerer Seiten heißt Parallelogramm.

Raute: Ein Parallelogramm mit vier zueinander kongruenten Seiten heißt Raute.
Ein Drache mit vier zueinandern kongruenten Seiten heißt Raute.
Ein Viereck mit vier zueinander kongruenten Seiten heißt Raute.

Rechteck: Ein Parallelogramm mit einem rechten Innenwinkel heißt Rechteck.
Ein rechtwinkliges Trapez mit einem weiteren Paar zueinander paralleler Seiten heißt Rechteck.
Ein Trapez mit einem weiteren Paar zueinander paralleler Seiten und einem rechten Innenwinkel heißt Rechteck.
Ein Viereck mit jeweils zwei gegenüberliegender paralleler Seiten und einem rechten Innenwinkel heißt Rechteck.

Quadrat: Eine Raute mit einem rechten Innenwinkel heißt Quadrat.
Ein Rechteck mit vier kongruenten Seiten heißt Quadrat.
Ein Viereck mit vier kongruenten Seiten und einem rechten Innenwinkel heißt Quadrat.

--Löwenzahn 15:15, 26. Mai 2010 (UTC)

Was bedeutet, eine Definition ist richtig?

Sie werden so allgemein die die Frage nach der Korrektheit Ihrer Definitionen nicht beantworten können. Sie müssen dann schon ein gewisses "Beziehungsgeflecht" der Definitionen angeben. Sie wissen ja "Es kann nur eine geben", die in einem anderen "Bezugsrahmen" wiederum durch eine andere Definition ersetzt werden kann". Am Besten nehmen Sie für Ihr Beziehungsgeflecht der Viereckdefinitionen das Haus der Vierecke als Grundlage. Sie werden eine völlig korrekte Antwort auf Ihre Fragen erst geben können, wenn jweils auch klar ist, wie Sie den jeweiligen Oberbegriff konkret definiert haben. Hie noch mal das Haus der Vierecke:

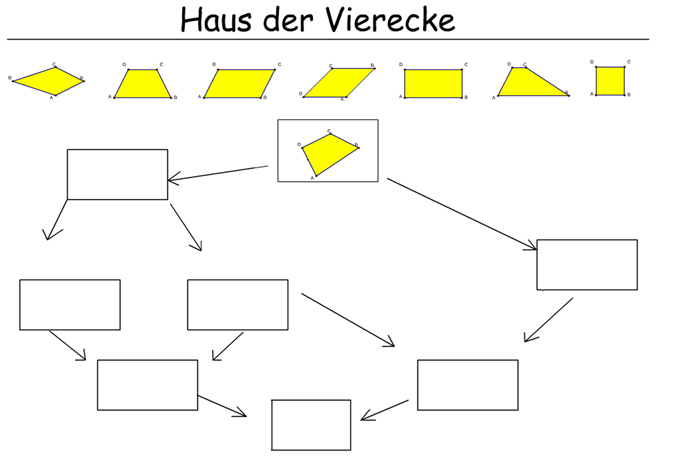
| zur Flash-Applikation --*m.g.* 07:43, 29. Mai 2010 (UTC)

Gruß

Vielen Dank für den Gruß. Es war schön in Leipzig - und hatte mal so überhaupt nix mit Mathematik zu tun. ;-) --Spannagel 11:16, 26. Mai 2010 (UTC)

Ellipse

In der pdf zur Mengenlehre steht unter 0.1.2. zur Ellipse, dass die Bedingung "Betrag von F1P + Betrag von F2P = Betrag von 2r" bei einer Ellipse erhalten bleibt. Der "Betrag von r" soll "die Länge eines beliebigen Radius von k" (Kreis) sein. Ist mit 2r im Falle der Ellipse dann der ursprüngliche Radius des Kreises gemeint, bevor man F2 verschoben hat? Weil eine Ellipse hat doch gar keinen Radius... Soll das eine Definition sein, oder sich auf eine bestimmte Ellipse beziehen? --Kuckuck 19:01, 2. Mai 2010 (UTC)

Es ist, wie du sagst: 2r ist der ursprüngliche Radius des Kreises. Es bezieht sich aber trotzdem allgemein auf alle Ellipsen. Der Unterschied der Ellipsen mit gleichem r liegt nur im Abstand zwischen F₁ und F₂.

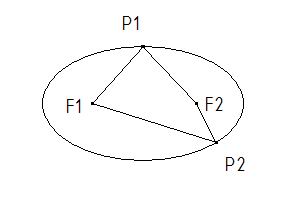
F₁P₁ und F₂P₁ haben die Länge r. Für P₂ gilt das natürlich nicht entsprechend. Aber die die Summe der Längen von F₁P₂ und F₂P₂ ist trotzdem 2r. --Sternchen 16:24, 7. Mai 2010 (UTC)

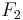Vielleicht hilft das: Sie können $\ P$ und $F_2$ manipulieren.

--*m.g.* 14:33, 10. Mai 2010 (UTC)--*m.g.* 14:33, 10. Mai 2010 (UTC)

Parallele Sonnenstrahlen?

Wir haben uns gestern in der Vorlesung mit der Bestimmung des Erdumfangs nach Eratosthenes beschäftigt. Dabei kam die Frage auf, woher Eratosthenes wusste, dass die Sonnenstrahlen annähernd parallel auf die Erde treffen. Schließlich wusste er noch nichts über Größe und Abstand der Sonne von der Erde. Hat jemand eine Idee? --Schnirch 10:08, 20. Apr. 2010 (UTC)

Hm... also ich hoffe ich mache das richtig, wenn ich hier meine Idee hinschreibe. Vllt. hat er den Schatten eines Gegenstandes mit geraden, parallelen Kanten aufgestellt (ich habe es mit einer Streichholzschachtel probiert) und dessen Schatten beobachtet. Die Kanten, die bei dem Gegenstand parallel sind, sind nun auch bei dem entstandenen Schatten parallel. Da die Lichtstrahlen für den Schatten verantwortlich sind, müssen sie auch parallel verlaufen.--Andreas 18:41, 20. Apr. 2010 (UTC)

ja, hier ist der richtige Platz für Ihre Ideen, vielen Dank für Ihre Antwort! Ich finde Ihre Idee sehr schön. Das Schattenbild eines Gegenstandes, das z. B. durch eine punktförmige Lichtquelle angestrahlt wird hat tatsächlich die Eigenschaft, dass die Schatten paralleler Kanten, die nicht parallel zur Bildebene liegen, sich im sogenannten Fluchtpunkt schneiden. Allerdings stellt sich mir die Frage, ab welcher Gegenstandsgröße dies nachweisbar wäre. Wir haben es hier ja mit Beobachtungen zu tun, die sehr weit auseinander liegen (Alexandria - Assuan). --Schnirch 12:43, 21. Apr. 2010 (UTC)

Am Bildschirm lesen

WEB2.0 ist für Leute, die zu blöd sind, sich selbst eine HTML-Seite zu generieren. So war meine Meinung bisher. Das Ganze hat auch damit zu tun, dass ich nicht gern am Bildschirm lese. Letztlich drucke ich mir lieber ein PDF aus, als dass ich längere Passagen am Bildschirm lese. Vielleicht ist das ja bei mir auch altersbedingt.--*m.g.* 03:46, 29. Apr. 2010 (UTC)

Ja, das könnte altersbedingt sein. ;-)) --Spannagel 08:41, 2. Mai 2010 (UTC)

Langsam gewöhne ich mich daran. Mein Monitor geht allerdings kaputt, weil ich ständig versuche, eine Ecke als Lesezeichen umzuknicken.--*m.g.* 12:19, 9. Jun. 2010 (UTC)

Felix Klein

Was meinen Sie hierzu?

„Soll ich mich im allgemeinen Sinne über Pädagogik äußern, so will ich folgende Betrachtung vorausschicken: Man kann das pädagogische Problem mathematisch formulieren, indem man die individuellen Qualitäten des Lehrers und seiner n Schüler als ebensoviele Unbekannte einführt und verlangt, eine Funktion von (n + 1) Variablen F(x0,...,xn) unter gegebenen Nebenbedingungen zu einem Maximum zu machen. Ließe sich dieses Problem eines Tages entsprechend den bisher realisierten Fortschritten der psychologischen Wissenschaft direkt mathematisch behandeln, so wäre die (praktische) Pädagogik von da ab eine Wissenschaft, — solange das aber nicht der Fall ist, muß sie als Kunst gelten."

(F. Klein (1849 - 1926) in seinem Vortrag: „Über Aufgabe und Methode des mathematischen Unterrichts an Universitäten")

Begriffsklärung

In der gestrigen Vorlesung bei Herrn Gieding fiel auf, dass er die Begriffe gleichlang sowie kongruent "anders" verwendet als Herr Schnirch. Daher sollte geklärt werden, ob wir die beiden Wörter als gleichwertige Synonyme gebrauchen oder ob kongruent mathematisch korrekter, d. h. formaler, als gleichlang ist.

Rückfrage: Was bedeuten die Aussagen "zwei Dreiecke sind kongruent" und "zwei Dreiecke sind gleichlang"? --Spannagel 08:42, 2. Mai 2010 (UTC)

Die erste Aussage bedeutet für mich, dass es sich um 2 deckungsgleiche Dreiecke handelt. Mich irritiert die zweite Aussage. Eventuell kann man von "gleichgroßen" Dreiecken sprechen (d. h. bedeutungsgleich zur ersten Aussage) - aber gleichlang? Bei z. B. Strecken würde ich den Begriff verwenden, aber nicht bei Flächen oder Körpern. --Pünktchen 16:16, 2. Mai 2010 (UTC)

@Spannagel und für alle die am Freitag nicht dabei waren: Die Problematik bezog sich auf die Kongruenz von Strecken und Winkeln.--*m.g.* 18:21, 2. Mai 2010 (UTC)

Wenn zwei Strecken gleichlang sind, dann sind sie kongruent. D.h. wenn man von Strecken spricht, dann kann man die Begriffe "kongruent" und "gleichlang" gleichsetzen. Dies geht auch direkt aus der Definition der Streckenkongruenz hervor (ich hoffe ich habe sie noch richtig im Kopf): "Zwei Strecken $\overline{AB}$ und $\overline{CD}$ sind kongruent, wenn der Abstand AB gleich dem Abstand CD ist (Abstände normalerweise mit Betragsstrichen und da auch meine Frage... wie macht man die hier :-) ). Bei Winkeln kann man ebenso "gleichgroß (haben das gleiche Maß)" und "kongruent" beliebig austauschen.--Andreas 16:56, 3. Mai 2010 (UTC)

Ich denke, wir sind uns alle in etwa einig, was die Begriffe bedeuten bzw. was wir damit bezeichnen. Die Frage richtet sich allerdings mehr auf die Klassifizierung. Soll heißen, dass einer der beiden Dozenten um eine verbindliche Aussage gebeten wird, ob für uns kongruent formal und gleichlang informell (Schnirch) oder beides formal ist (Gieding). Es gibt nicht wenige Studenten, die beide Veranstaltungen besuchen und dementsprechend verwirrt sind. Vielen Dank!

An dieser Diskussion zeigt sich sehr schön, dass es bei Definitionen nicht um richtig oder falsch sondern um sinnvoll oder nicht sinnvoll geht und man sich darüber einigen muss wie man bestimmte Begriffe in ein System einordnet. Einigen wir uns darauf, dass wir die Begriffe "gleichlang" und "kongruent" synonym verwenden dürfen. Wir verwenden also ab sofort beide Begriffe im Rahmen formaler Definitionen.--Schnirch 17:50, 5. Mai 2010 (UTC)

Zur grundlegenden Idee der Veranstaltung "Definieren":
Wir sahen es als sinnvoll an, eine Veranstaltung nur für das Definieren einzurichten. Eine solche Veranstaltung bietet sich gleichzeitig für didaktische Bemerkungen bezüglich der Verwendung von Begriffen und deren Erklärungen/Festlegungen/Definitionen im Mathematikunterricht an. Aus diesem Grunde wurde der Spannungsbogen informelle Definition vs. formale Definition angesprochen. Die Idee der informellen Definition ist didaktischer Natur. Ebenso erfolgt die Einteilung von Definitionen in informelle und formale Definitionen rein aus didaktischer Sicht. Der reine Mathematiker kennt weder informelle noch formale Definitionen, er kennt nur Definitionen. Aus didaktischer Sicht sind die Grenzen zwischen informellen Definitionen und formalen Definitionen fließend und von verschiedenen Parametern, wie etwa dem Alter der Schüler, abhängig.
Wie auch immer, wir wollen in der Einführung in die Geometrie nicht nur gewisse Definitionen kennen lernen, sondern vor allem das Definieren lernen. Lernen Sie keine Definitionen auswendig, sondern entwickeln Sie Ihre Fähigkeiten bezüglich des Definierens. --*m.g.* 11:14, 6. Mai 2010 (UTC)

Was ist damit wohl gemeint?

Viele Grüße von den Donnerstagsmedienspezialisten