Diskussion:Lösung von Aufgabe 5.3 (SoSe11)
Wir gehen von folgender Implikation aus: Wenn zwei Geraden g und h nicht identisch sind, dann haben sie höchstens einen Punkt gemeinsam.
a) Wie lautet die Kontraposition dieser Implikation?
b) Wie lautet die Annahme, wenn Sie diese Implikation durch einen Widerspruch beweisen möchten?
Antwort:
a) Wenn zwei Geraden höchstens einen gemeinsamen Punkt haben, sind sie nicht identisch.
b) Annahme: Es gibt Geraden, die nicht identisch sind und dennoch mehr als einen gemeinsamen Punkt haben.
--Bubble 13:46, 5. Mai 2011 (CEST)
a) Wenn zwei Geraden g und h identisch sind, dann haben sie mindestens einen Punkt gemeinsam.
b) Es gibt zwei Geraden, die nicht identisch sind und mehr als einen Punkt gemeinsam haben. --Flo 21 14:42, 5. Mai 2011 (CEST)
Was ist nun bei a) richtig, oder stimmen beide Antworten? Wie wird der Begriff "Kontraposition" verstanden bzw. wie ist er definiert?--Tutor Andreas 13:32, 6. Mai 2011 (CEST)
An den lieben Tutor: Treffe doch bitte die Aussage, ob jmd recht hat oder nicht und verbessere gegebenenfalls. Deine Antworten sind max. bedingt hilfreich. So bringt mich das WIKI nicht weiter, es behindert mich. Schließlich merkt man sich so evtl falsche Sachen. Danke. --Flo 21 19:50, 8. Mai 2011 (CEST)
Ich würde mich Flo21 anschließen. Die Antwort von Bubble ist die Umkehrung und nicht die Kontraposition. --Matthias 19:08, 8. Mai 2011 (CEST)
Ich bin der Meinung, dass man sich zu den Aussagen von anderen auch Gedanken machen sollte und diese dann diskutiert. Wenn es aber erwünscht wird, dass die Antworten mit RICHTIG oder FALSCH gekennzeichnet werden, dann werde ich mit einem Dozenten besprechen, wann und wie dies geschehen soll. Dies sollte aber auch nicht auf dieser Seite stehen, sondern auf einer allgemeinen Diskusionsseite. --Tutor Andreas 20:27, 9. Mai 2011 (CEST)
Tutor Andreas und auch Tutorin Anne machen das mit der Hilfestellung aus meiner Sicht genau richtig - und zwar so, wie Sie optimal beim Prozesslernen
von Mathematik unterstützt werden. Es ist ganz wichtig, dass Sie sich Ihre eigenen Gedanken machen (was auch super klappt)
und durch den Austausch mit Anderen gemeinsam auf die richtige Spur gelangen - auch das lässt sich hier im Wiki schon sehr schön beobachten!
Übrigens behandeln wir die Aufgabenserie 5 erst diese Woche in den Übungen, d. h. es macht zu diesem Zeitpunkt wirklich noch keinen Sinn
Ergebnisse bekannt zugeben.--Schnirch 14:55, 10. Mai 2011 (CEST)
Ich schließe mich auch FLo 21 an, würde aber zu a) hinufügen wollen, dass die Geraden mehr als einen Punkt bzw. mindestens zwei Punkte gemeinsam haben. Wie Flo 21 auch in b) formuliert. -> Welche Version davon ist richtig? Oder macht dies keinen Unterschied?
Zu der Aussagelautet die Kontraposition
. --Tutor Andreas 20:59, 9. Mai 2011 (CEST)
Mein Lösungsvorschlag zu Aufgabe a): Wenn zwei Geraden mehr als einen gemeinsamen Punkt haben, dann sind sie identisch. --KlaraM 16:31, 10. Mai 2011 (CEST)
Ich habe die Lösung genau wie Klara, wir müssen ja schließlich beides verneinen. --Fledermaus 17:45, 10. Mai 2011 (CEST)
Ich schließe mich auch Klara und fledermaus an, denn die Umkehrung muss verneint werden und diese lautet: wenn 2 geraden g ung h höchstens einen punkt gemeinsam haben, dann sind sie nicht identisch. somit muss die kontrapostion der von klara entsprechen.--CarinaW 21:22, 11. Mai 2011 (CEST)
Bemerkung von --*m.g.* 23:45, 11. Mai 2011 (CEST):
- @CarinaW: Klingt vielleicht spitzfindig, ist aber doch sehr wichtig: Die Kontrapostion einer Implikation erhält man nicht dadurch, dass dass man die Umkehrung dieser Implikation negiert. Sie meinen das ganz bestimmt nicht. Aber in der Mathematik zählt nur das was geschrieben wurde (ich überspitzte):
- Unsere Implikation lautet:
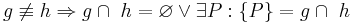 .
.
- Die Negation dieser Implikation lautet:
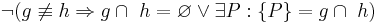 .
.
- Besser verständlich formuliert: Es gilt nicht: Wenn die Geraden
 und
und  nicht identisch sind, dann haben sie höchstens einen Punkt gemeinsam.
nicht identisch sind, dann haben sie höchstens einen Punkt gemeinsam.
- Jetzt zur Umkehrung: Voraussetzung wird Behauptung und umgekehrt:
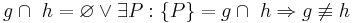
- Einfacher ausgedrückt: Wenn zwei Geraden
 und
und  höchstens einen Punkt gemeinsam haben, dann sind sie nicht identisch.
höchstens einen Punkt gemeinsam haben, dann sind sie nicht identisch.
- Die Negation dieser Umkehrung: Es gilt nicht: Wenn zwei Geraden
 und
und  höchstens einen Punkt gemeinsam haben, dann sind sie nicht identisch.
höchstens einen Punkt gemeinsam haben, dann sind sie nicht identisch.
- Diese Negation ist wie man leicht sieht nicht wahr. Wir brauchen auch nicht die Negation der Umkehrung sondern die Kontraposition:
- Negation(
 und
und  haben höchsten einen Punkt gemeinsam)
haben höchsten einen Punkt gemeinsam)  Negation(Die Geraden sind nicht identisch).
Negation(Die Geraden sind nicht identisch).
- Lange Rede kurzer Sinn: Sie haben sicherlich nicht die Negation der Umkehrung gemeint, sondern die Negation der Voraussetzung der Umkehrung und die Negation der Behauptung der Umkehrung.
- @CarinaW: Klingt vielleicht spitzfindig, ist aber doch sehr wichtig: Die Kontrapostion einer Implikation erhält man nicht dadurch, dass dass man die Umkehrung dieser Implikation negiert. Sie meinen das ganz bestimmt nicht. Aber in der Mathematik zählt nur das was geschrieben wurde (ich überspitzte):

