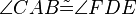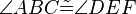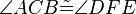Dreieckskongruenz WS 11/12
Inhaltsverzeichnis
|
Die beiden grundlegenden Ideen der Kongruenz =
Bewegungsgeometrie
naive Deckungsgleichheit
Bewegungen: abstandserhaltende Abbildungen der Ebene auf sich
Euklid lässt grüßen: Dreieckskongruenz
Videos zur Idee der Kongruenz
Streckenkongruenz
Wir erinnern uns an die Diskussion zu Anfang des Semesters.
Die Auswertung des Quiz zeigt: Alle drei Aussagen sind synonym.
Momentan jedoch eigentlich noch nicht. Uns fehlt eine Definition des Begriffs der Streckenkongruenz.
Definition VII.1: (Streckenkongruenz)
- Zwei Strecken sind kongruent, wenn sie dieselbe Länge haben.
- In Zeichen
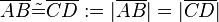
- Zwei Strecken sind kongruent, wenn sie dieselbe Länge haben.
Satz VII.1:
- Die Relation kongruent ist auf der Menge aller Strecken eine Äquivalenzrelation.
Der Beweis ergibt sich unmittelbar durch Rückführung auf die Gleicheitsrelation auf der Menge der reellen Zahlen.
Winkelkongruenz
Analog zum Begriff der Streckenkongruenz sollen zwei Winkel genau dann kongruent zueinander genannt werden, wenn sie dieselbe Größe haben.
Definition VII.2 : (Winkelkongruenz)
- Zwei Winkel die dieselbe Größe haben heißen kongruent zueinander.
- In Zeichen:
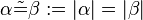
- Zwei Winkel die dieselbe Größe haben heißen kongruent zueinander.
Satz VII.2:
- Die Relation kongruent ist auf der Menge aller Winkel eine Äquivalenzrelation.
Der Beweis ergibt sich unmittelbar durch Rückführung auf die Gleicheitsrelation auf der Menge der reellen Zahlen.
Dreieckskongruenz
In der Schule spricht man häufig davon, dass zwei Dreiecke dann kongruent zueinander sind, wenn sie in allen Stücken übereinstimmen. Unter den Stücken eines Dreieck sind dabei die jeweils drei Seiten und die jeweils drei Innenwinkel zu verstehen.
Definition VII.3: (Dreieckskongruenz)
- Wenn für zwei Dreiecke
 und
und  die folgenden 6 Kongruenzen
die folgenden 6 Kongruenzen
- Wenn für zwei Dreiecke
- gelten,
- dann sind die beiden Dreiecke
 und
und  kongruent zueinander.
kongruent zueinander.
Satz VII.3:
- Die Relation kongruent ist auf der Menge aller Dreiecke eine Äquivalenzrelation.
Der Beweis ergibt sich unmittelbar durch Rückführung auf die Gleicheitsrelation auf der Menge der reellen Zahlen.
Überprüfen Sie Ihr Verständnis:
In den Schullehrbüchern findet man häufig Konstruktionsaufgaben wie:
konstruiere das Dreieck mit den Seitenlängen 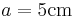 ,
, 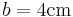 ,
, 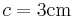 .
. 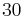 Schüler konstruieren aufgrund dieser Aufgabenstellung
Schüler konstruieren aufgrund dieser Aufgabenstellung 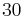 Dreiecke. Kommentieren Sie den bestimmten Artikel in der Aufgabenstellung. Was hat das alles mit der Idee der Repräsentantenunabhängigkeit zu tun?
Dreiecke. Kommentieren Sie den bestimmten Artikel in der Aufgabenstellung. Was hat das alles mit der Idee der Repräsentantenunabhängigkeit zu tun?
Das Kongruenzaxiom SWS
Axiom V: (Kongruenzaxiom SWS)
- Wenn für zwei Dreiecke
 und
und  die folgenden 3 Kongruenzen
die folgenden 3 Kongruenzen
- Wenn für zwei Dreiecke
- gelten,
- dann sind die beiden Dreiecke
 und
und  kongruent zueinander.
kongruent zueinander.
Der Kongruenzsatz WSW
Satz VII.4: (Kongruenzsatz WSW)
- Wenn für zwei Dreiecke
 und
und  die folgenden 3 Kongruenzen
die folgenden 3 Kongruenzen
- Wenn für zwei Dreiecke
- gelten,
- dann sind die beiden Dreiecke
 und
und  kongruent zueinander.
kongruent zueinander.
Beweis von Satz VII.4
Als Folge von Tafeln
Video
Die Beweisidee
Testen Sie Ihr Verständnis: Beschreiben Sie hier mit drei ganz einfachen Sätzen, auf welcher Idee der Beweis beruht.
Der Kongruenzsatz SSS
Hier dürfen und sollen Sie sich austoben. Für den Beweis des Kongruenzsatzes SSS werden Sie sinnvollerweise den Basiswinkelsatz benötigen. Weil dieser jedoch von so zentraler Bedeutung ist, haben wir ihm einen eigenen Unterpunkt auf der Hauptseite spendiert. Sie dürfen ihn also hier vorab als wahr voraussetzen.
Beweisidee I
Zwei Dreiecke ABC und DEF sind zueinander kongruent, wenn sie in allen drei Seiten übereinstimmen.
Vor.:
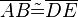
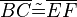
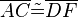
Beh.: 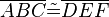
Beweis:
| Überschrift 1 | Überschrift 2 |
|---|---|
(1)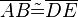 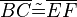 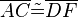 |
Vor. |
(2) 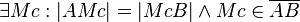 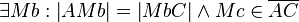 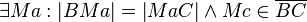 |
Existenz und Eindeutigkeit des Mittelpunkts einer Strecke |
(3) 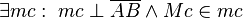 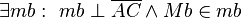 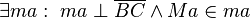 |
Existenz und Eindeutigkeit der Mittelsenkrechten (2) |
(4) 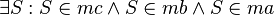 |
Schnittpukt der Mittelsenkrechten (3) |
(5) 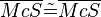 |
trivial |
(6) 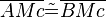 |
M ist Mittelpunkt (2) |
(7) 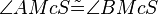 |
rechter Winkel, Mittelsenkrechte (3) |
(8) 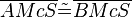 |
(5)(6)(7) SWS |
(9) 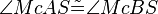 |
(8) |
(10) 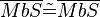 |
trivial |
(11) 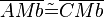 |
M ist Mittelpunkt (2) |
(12) 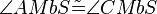 |
rechter Winkel, Mittelsenkrechte (3) |
(13) 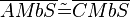 |
(10)(11)(12) SWS |
(14) 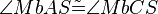 |
(13) |
(15) 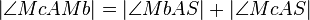 |
(9),(14) Winkeladditionsaxiom |
(16) Schritte (2) bis (15) analog mit Dreicek  |
|
(17) 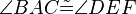 |
(15),(16) |
(18) 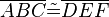 |
(17), Vor., SWS |
Den Beweisschritten konnte ich soweit folgen. Allerdings ist Schritt (17) nicht aus den vorrigen Schritten ableitbar.
(Du hast davor für zwei Dreiecke gezeigt, dass bestimmt Seiten/ Winkel kongruent sind, bestimmte Innendreiecke usw. Allerdings hast du keine Kongruenz zwischen Innendreiecke der verschiedenen Dreiecke ABC und DEF gezeigt. Somit kannst du auch nicht auf die Winkel schließen. - Falls du es versuchen willst, die inneren Dreiecke aufeinander zu beziehen, wird es schon damit scheitern, dass du nicht weißt, ob der Schnittpunkt der Mittelsenkrechten die gleiche Entfernung in beiden Dreiecken z.B. zu den Seiten des Dreiecks hat. )
Ich glaube nicht, dass der Ansatz dir weiter hilft - sorry. Trotzdem: Danke für den Beitrag ... so lernen wir gemeinsam.--Tutorin Anne 20:45, 12. Jan. 2012 (CET)
Aber wenn doch die Seiten konguent sind, müssen es die die davon abgeleiteten Mittelsenkrechten auch sein. Ich meine damit , ich beziehe mich immer auf die Steken zunächst eines Dreiecks, die Stecken beider Dreiecke sind aber Konguent laut Vorrausetzung, also müssen sämtliche Innendreiecke auch konguent sein. Da ich die Mittelsenkrechen nur auf die Jeweiligen Strecken beziehe. Somit muss der Schnittpunkt der Mittelsenkrechten auch konguent sein (siehe Geogebra sktize). Also wo ist mein Denkfehler?--RicRic 21:45, 12. Jan. 2012 (CET)
Kann ich bis einschließlich Punkt 4 davon ausgehen, dass dies bei beidens Dreieken gleich ist. Also der Schnittpunkt der Mittelsenkrechten somit bei beiden Dreieken identisch ist. Da ich mich ja auf das Mittelsenkrechtenkriterium berufe und dies müsste ja für jede Strecke eindeutig sein, somit auch für den Schnittpunkt der Mittelsenkrechten, oder?--RicRic 20:50, 16. Jan. 2012 (CET) Warum sollte der Schnittpunkt der Mittelsenkrechten in beiden Dreiecken identisch sein, wenn diese vielleicht gar nicht kongruent sind? Das Problem an dem Beweis ist, dass du innerhalb eines Dreicks viel zeigst, aber es geht um den Vergleich, um Kongruenzen zum anderen Dreieck.
Da sehe ich die Schwierigkeit--Tutorin Anne 10:48, 18. Jan. 2012 (CET)
Beweisidee II
Vor.:
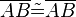
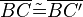
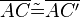
Beh.: 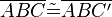
Beweis:
| Schritt | Begründung |
|---|---|
(1)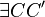 |
Axiom I2 Gerade durch zwei Punkte |
(2) 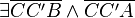 |
(1) |
(3)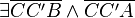 sind gleichschenklig, da sind gleichschenklig, da 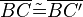 und und 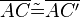 |
nach Vorr (2) |
| (4) es gelten konguente Winkel siehe Skizze | Basiswinkelsatz, (3) |
(5) 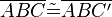 |
SWS, Winkeladditionsaxiom, Rechnen in R,Vorr. (4) |
Der Beweis ist soweit korrekt, allerdings habt ihr damit auch wirklich nur diese spezielle Behauptung beweisen. Also nicht allgemein den SSS-Kongruenzsatz. Dazu müsst ihr von zwei Dreiecken ausgehen, die keine gemeinsame Strecke haben müssen. --Tutorin Anne 20:33, 12. Jan. 2012 (CET)
Aber wenn die Stecken konguent ist, dann kann ich sie doch durch drehen oder spiegeln oder verschieben genau auf der andern Stecke abbilden, warum darf ich das hier nicht?--RicRic 21:47, 12. Jan. 2012 (CET)
Du kannt die Beweisidee so verwenden für ein allgemeinen Beweis. Dazu musst du aber von Anfang an von zwei komplett verschiedenen Dreiecken ausgehen, nicht von Dreiecken die eine Seite gemeinsam haben. Das ist aber nicht viel zu ändern.--Tutorin Anne 10:43, 18. Jan. 2012 (CET)
Aber die Idee funktioniert doch nur weil ich eine gemeinsame Seite habe und diese teile, sehe nicht wie sich sonst die gleichschenkligen Dreieke sonst hinbekommen soll.--RicRic 20:39, 18. Jan. 2012 (CET)
weitere Beweisideen
Vor.: 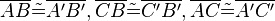
Beh.: 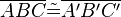
Beweis:
| Überschrift 1 | Überschrift 2 |
|---|---|
(1) 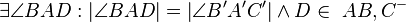 |
Winkelmaßaxiom, Winkelkonstruktionsaxiom |
(2) 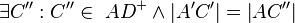 |
Abstsaxiom, Axiom vom Lineal |
(3) 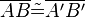 |
Vorr |
(4) 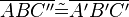 |
SWS, (1),(2),(3) |
(5) 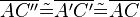 |
Vor, (2) |
(6) 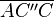 ist gleichschenklig ist gleichschenklig |
(5) |
(7) 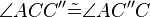 |
Basiswinkelsatz (6) |
(8) 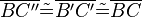 |
Vor, (4) |
(9) 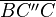 ist gleichschenklig ist gleichschenklig |
(8) |
(10) 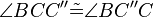 |
Basiswinkelsatz (9) |
(11) 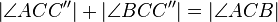 |
Winkeladitionosaxiom (7),(10) |
(12) 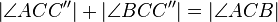 |
Winkeladitionosaxiom (7),(10) |
(13) 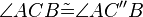 |
Rechen in R (11),(12) |
(14) 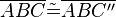 |
Vor. (13) SWS |
(15) 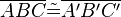 q.e.d. q.e.d. |
(14),(4) |
Nach dem ich es dann visualisiert habe, habe ich es wieder nachvollziehen können. Gut!
(Die ersten Schritte der Applikation sind für den Beweis unwichtig. Ich musste nur erst mal die Voraussetzung konstruieren (wobei ich darauf zurückgegriffen habe, dass die Behauptung stimmt :)). --Tutorin Anne 12:55, 25. Jan. 2012 (CET)
Prima, dann können wir ja den SsW angehen.--RicRic 17:42, 25. Jan. 2012 (CET)
...
ja dann, viel Freude!--Tutorin Anne 18:27, 25. Jan. 2012 (CET)
SsW-Kongruenzsatz
Vor:  ;
; 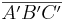
1. 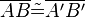 ;
;
2. 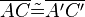 ;
;
3. 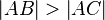 ;
;
4. 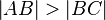 ; Dies muss nicht gelten! --Tutorin Anne 17:52, 29. Jan. 2012 (CET)
; Dies muss nicht gelten! --Tutorin Anne 17:52, 29. Jan. 2012 (CET)
5. 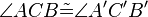
Beh.: 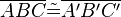
Es genügt zu zeigen, dass, da nach SSS die Dreiecke dann kongruent sind. --Tutorin Anne 17:52, 29. Jan. 2012 (CET)
Ann.: o.B.d.A. 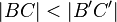 Beweis:
Beweis:
| Überschrift 1 | Überschrift 2 |
|---|---|
(1) 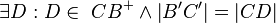 |
Axiome Abstand und Lineal |
(2) 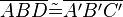 |
SWS, (1), Ann., Vor2, Vor5 |
(3) 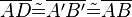 |
(2), Vor.1 |
(4) 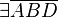 |
(1),Ann. |
(5) 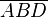 ist gl.schenklig ist gl.schenklig |
(3) |
(6) 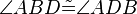 |
(5) Basiswinkelsatz |
(7) 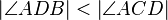 |
Vor3, Vor4, Satz der gr. Seite liegt der gr. Winkel gegenüber |
(8) 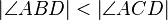 Wiederspruch zu (6) und (7) Ann verwerfen Beh., Stimmt, betrift auch das Deieck A'B'C' wegen (2) |
schwacher Ausenwinkelsatz, ist Außenwikel von 
|
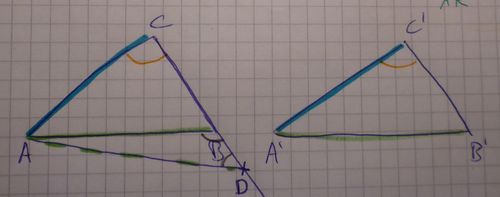
Sehr gut! Mit Skizze lässt sich dein Beweis gut nachvollziehen. Allerdings musst du die Begründung für Schritt (7) noch ändern, denn Vor4 gibt es leider nicht!--Tutorin Anne 17:52, 29. Jan. 2012 (CET)
Die Dreieke müssen in dem Winkel übereinstimmen, der der längeren Seite gegenüber liegt. Somit Reicht mir doch als Begründung für Schritt (7) die Vor3. --RicRic 19:15, 31. Jan. 2012 (CET)