Lösung von Aufg. 11.2 (WS 11/12)
Aus Geometrie-Wiki
Beweisen Sie Satz VI.eineinhalb
- Es sei
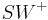 die Winkelhalbierende des Winkels
die Winkelhalbierende des Winkels  . Dann gilt
. Dann gilt 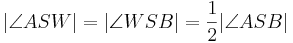 .
.
- Es sei
Vor.: Es sei 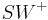 die Winkelhalbierende des Winkels
die Winkelhalbierende des Winkels 
Beh.: 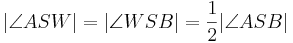
Beweis:
| Schritt | Begründung |
|---|---|
(1)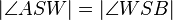 |
Definiton Winkelhalbierende |
(2) W im inneren von  |
Definiton Winkelhalbierende |
(3) 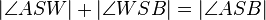 |
(1),(2),Winkeladditonsaxiom |
(4) 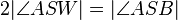 |
(1),(3) |
(5) 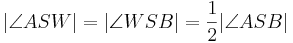 |
(4) Rechnen in R |

