Lösung von Aufg. 6.7 (WS 11/12)
Es seien 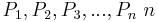 verschiedene Punkte der Ebene, von denen je drei stets nicht kollinear sind. Wie viele verschiedene Geraden gibt es, die jeweils durch zwei dieser
verschiedene Punkte der Ebene, von denen je drei stets nicht kollinear sind. Wie viele verschiedene Geraden gibt es, die jeweils durch zwei dieser  Punkte gehen?
Hinweis: Es gibt eine Problemlösestrategie: Führe einen komplizierten Fall auf einen einfacheren Fall zurück. Carl Friedrich Gauß hilft auch bei der Lösung dieser Aufgabe.
Punkte gehen?
Hinweis: Es gibt eine Problemlösestrategie: Führe einen komplizierten Fall auf einen einfacheren Fall zurück. Carl Friedrich Gauß hilft auch bei der Lösung dieser Aufgabe.
Im Praktikum haben wir eine analoge Aufgabe einmal mit Schülern einer 7. Hauptschulklasse gelöst. Formulieren Sie obige Aufgabe für Schüler dieser Schulstufe.
| Punkte | mögl. Geraden |
|---|---|
| 3 | 3(1+2) |
| 4 | 6(3+3) |
| 5 | 10(6+4) |
| 6 | 15(10+5) |
| 7 | 21(15+6) |
| 8 | 28(21+7) |
| ... | ... |
Kommt also ein weiter Punkt hinzu, erhalte ich die aktuelle Menge der Geraden durch die Menge der bisher vorhanden Geraden plus die Zahl der bisher vorhanden Punkte.
(n-1)!--RicRic 21:36, 21. Nov. 2011 (CET)
- aber mit (n-1)! klappt das ab 5 nicht mehr. BeaBer und ich haben uns überlegt, dass es mit der Formel:
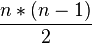 klappen könnte, mit Anlehnung an Gauß :)--Miriam 13:00, 22. Nov. 2011 (CET)
klappen könnte, mit Anlehnung an Gauß :)--Miriam 13:00, 22. Nov. 2011 (CET)
Vielleicht hilft das:--*m.g.* 15:06, 22. Nov. 2011 (CET)
[ www.ph-heidelberg.de is not an authorized iframe site ]

