Lösung von Aufg. 7.4 (WS 11/12)

Das Axiom I.7 sagt aus:

Es gibt vier Punkte, die nicht komplanar sind.

Es sei $\ \epsilon$ eine beliebige Ebene und $\ A, B, C, D$ die vier Punkte entsprechend Axiom I.7. Klassifizieren Sie alle Fälle die bezüglich der Inzidenz der Punkte $\ A, B, C, D$ mit $\ \epsilon$ auftreten können.

o.B.d.A:
Fall 1: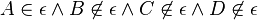$A\in \epsilon \wedge B\not\in \epsilon \wedge C\not\in \epsilon \wedge D\not\in \epsilon$
Fall 2: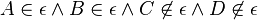$A\in \epsilon \wedge B\in \epsilon \wedge C\not\in \epsilon \wedge D\not\in \epsilon$
Fall 3: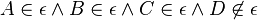$A\in \epsilon \wedge B\in \epsilon \wedge C\in \epsilon \wedge D\not\in \epsilon$
Fall 4: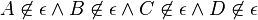$A\not\in \epsilon \wedge B\not\in \epsilon \wedge C\not\in \epsilon \wedge D\not\in \epsilon$ --RicRic 12:33, 4. Dez. 2011 (CET)