Lösung von Aufg. 8.5 (SoSe 11)

Satz:

Von drei paarweise verschiedenen Punkten $\ A, B$ und $\ C$ ein und derselben Geraden $\ g$ liegt genau einer zwischen den beiden anderen.

Beweisen Sie diesen Satz.
Voraussetzung: A, B, C sind paarweie verschieden und liegen auf ein und derselben Gerade g
Behauptung: Ein Punkt B (o. B. d. A.) liegt zwischen den beiden anderen
Beweis durch Widerspruch:
Fall 1: Kein Punkt liegt zwischen zwei anderen
Annahme: |AB| = |AC| = |BC|

Auf der Diskussionsseite befindet sich noch ein Kommentar, der noch nicht näher diskutiert wurde und dies sollte evtl. geklärt werden Diskussion:Lösung von Aufg. 8.5 (SoSe 11)--Tutor Andreas 18:00, 6. Jun. 2011 (CEST)

1)	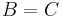$|AB| = |AC|$ $\Rightarrow$ $B = C$	Vor., Axiom II.2, Axiom II.1, Annahme
2)	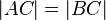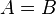$|AC| = |BC|$ $\Rightarrow$ $A = B$	Vor., Axiom II.2, Axiom II.1, Annahme
3)	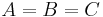$A = B = C$	(1), (2), Transitivität von "="
4)	Widerspruch zur Voraussetzung A, B, C paarweise verschieden; Annahme ist zu verwerfen	(3)

Fall 2: Zwei Punkte liegen zwischen zwei anderen
Annahme: Es gilt: Zw(A, B, C) und Zw(B, A, C)

1)	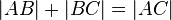$|AB| + |BC| = |AC|$	Def. ZWrel., Annahme
2)	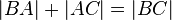$|BA| + |AC| = |BC|$	Def. ZWrel., Annahme
3)	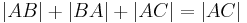$|AB| + |BA| + |AC| = |AC|$	Rechnen in R, (1), (2)
4)	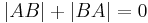$|AB| + |BA| = 0$	Rechnen in R, (3)
5)	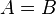$A = B$	Axiom II.1 (d als positive reele Zahl und wenn eine Zahl a mit einer anderen Zahl b addiert wird und Null ergibt, ist a=b=0), Axiom II.2
6)	Widerspruch zur Voraussetzung, paarweise verschieden	(5)

--Flo60 23:25, 31. Mai 2011 (CEST)

Ich glaube, es war relativ unwirtschaftliche, diesen beweis durch wiederspruch zu führen, da er sich ebenfalls und einfacher direkt beweisen lässt (und dann hätte sich auch die diskussion erledigt):

BEWEISVERSUCH II:

Voraussetzung: A, B, C sind paarweie verschieden und liegen auf ein und derselben Gerade g
Behauptung: 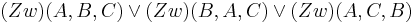$\operatorname(Zw) (A, B, C) \vee \operatorname(Zw) (B, A, C) \vee \operatorname(Zw)(A, C, B)$

1	Die Punkte A, B und C sind kollinear	Vorraussetzung, Definition kollinear
2	Es gilt: 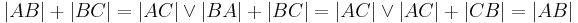$\left| AB \right| + \left| BC \right| = \left| AC \right| \vee \left| BA \right| + \left| BC \right| = \left| AC \right| \vee \left| AC \right| + \left| CB \right| = \left| AB \right|$	(1), Axiom II.3
3	Daraus folgt: 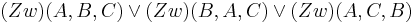$\operatorname(Zw) (A, B, C) \vee \operatorname(Zw) (B, A, C) \vee \operatorname(Zw)(A, C, B)$	(2), Def. Zwischenrelation

--Flo60 17:04, 17. Jun. 2011 (CEST)
Dieser Beweis ist natürlich wirtschaftlicher und er ist auch völlig korrekt. Allerdings entspricht die Behauptung nicht der Aufgabenstellung. Also, es wurde nicht gezeigt das genau eine der Zwischenrelationen gilt (das steht nämlich nicht im Axiom II.3). Das war im 1. Beweis richtig. --Tutorin Anne 10:52, 18. Jun. 2011 (CEST)

Das heißt, wenn ich jetzt noch zeige, dass keine zwei gleichzeitig gelten (was ich oben in Fall 2 berücksichtigt habe) wäre es ok, oder? weil dass ja eines keines zutrifft ist ja ausgeschlossen und wenn ich annehmen, dass zwei zutreffen und das negiere, müsste alles bewiesen sein, hoff ich :-)--Flo60 13:28, 18. Jun. 2011 (CEST)

Wenn man in der Behauptung o.B.d.A annimmt, dass Zw(A,B,C) und dann in der Annahme Zw(A,C,B) oder Zw(B,A,C) zum Widerspruch führt, dann muss ja o.B.d.A gelten, dass genau ein Punkt zwischen den beiden anderen liegt, d.h. genau eine Zwischenrelation gilt. Hier bin ich wie folgt vorgegangen: die Gleichungen aus Axiom II/3 lassen sich gleichsetzen und dann müsste AC=0 sein --> Widerspruch zur VSS, dass A ungleich C ist.--mm_l 15:40, 14. Jul. 2011 (CEST)

Lösungen der Gruppenarbeit aus der Übung Klara Buchner

• Die Lösung stimmt.