Lösung von Aufgabe 10.3P (SoSe 13)

Welche wichtige Erkenntnis ergibt sich aus Satz IX.2 für die absolute und relative Lage der beiden Spiegelgeraden? Nutzen Sie diese Erkenntnis für die Lösung der folgenden beiden Aufgaben.

Zu Satz IX.2: http://wikis.zum.de/geowiki/Verkettung_zweier_Geradenspiegelungen_SoSe_13#Satz_IX.2_:

• Für die verkettete Spiegelung 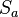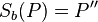$S_{a}$ ° $S_{b}(P) = P''$ ist ausschließlich der Schnittpunkt S der beiden Spiegelgeraden a,b und deren Winkel zueinander von Relevanz.--Nolessonlearned 13:27, 2. Jul. 2013 (CEST)
  
• Aha, und was könnte uns das bringen?--Tutorin Anne 10:31, 3. Jul. 2013 (CEST)
  
  • Das bedeutet, dass die Verketteten Spiegelachsen frei positionierbar sind, solange der Winkel zwischen den Achsen und deren Drehpunkt konstant bleibt.--Nolessonlearned 17:40, 13. Jul. 2013 (CEST)
    
    • Genau.--Tutorin Anne 09:17, 15. Jul. 2013 (CEST)

@ Nolessonlearnd: Die Striche bei P wurden nicht angezeigt, da zwei Striche das Ankündigung/ Abkündigungszeichen bei Latex fungiert. Deshalb habe ich deine Aussage zum mathematischen Ausdruck verändert. --Tutorin Anne 10:31, 3. Jul. 2013 (CEST)

• • Danke Anne

• ICH VERSTEH KOMPLETT DIE AUFGABE NICHT! ;-((( Den Satz kann ich nachvollziehen, aber was es mit der Absoluten und Relative Lage zu tun verstehe ich nicht- geschweige wie es aussehe soll. Im Leitfaden steht auch nichts darüber sowie im Internet. kann jemand mir irgendwie Ansatzweise erklären, was ich machen soll?--Blumenkind 15:16, 7. Jul. 2013 (CEST)Blumenkind 15.16, 7.Juli
  • Also, absolute Lage, heißt feste Lage - unveränderbar. Spiegelachsen dürfen aber in ihrer Lage verändert werden, aber nicht einfach irgendwie, sondern unter bestimmten Bedingungen, die Nolessonlearned genannt hat. Damit ist ihre Lage nicht beliebig, sonder relativ (in Relation zur anderen Spiegel-Gerade nämlich fest vorgegeben).--Tutorin Anne 14:59, 8. Jul. 2013 (CEST)