Lösung von Aufgabe 4.5P (SoSe 12)

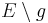Es seien eine Ebene E (aufgefasst als Punktmenge) und eine Gerade g in E gegeben. Wir betrachten folgende Relation $\ \Theta$ ($\ \Theta$ ist ein willkürlich gewähltes Symbol, um die Relation nicht mit dem unauffälligen Buchstaben R bezeichnen zu müssen) in der Menge $\ E \setminus g$ (also alle Punkte der Ebene E, die nicht der Geraden g angehören): Für beliebige 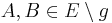$\ A,B \in E \setminus g$ gilt: $\ A \Theta B: \Leftrightarrow \overline{AB}\cap g = \lbrace \rbrace$.

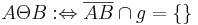Zurück zu: Übung_Aufgaben_4_P_(SoSe_12)

a) Beschreiben Sie die Relation $\ \Theta$ verbal und veranschaulichen Sie diese Relation.

Die Strecke AB geschnitten mit g ergibt eine leere Menge. --Malilglowka 17:48, 10. Mai 2012 (CEST)

veranschaulicht: da die strecke zwischen a und b die gerade g nicht schneiden darf, müssen beide punkte auf einer seite der durch die gerade g geteilten ebene e liegen
noch mehr veranschaulicht: ich habe eine ebene (ebene e)mit einer tiefen schlucht (gerade g): die strecke ab darf keine "brücke" über die canyonlücke (gerade g) der ebene bilden--Studentin 01:02, 11. Mai 2012 (CEST)

Für beliebige Punkte A, B, die in der Ebene E liegen, aber nicht auf der Geraden g liegen gilt: A steht in Relation zu B genau dann, wenn die Schnittmenge der Strecke AB und der Geraden g eine leere Menge ist (bzw. keine Elemente enthält).
Stimmt das so? --Honeydukes 20:53, 12. Mai 2012 (CEST)

b) Begründen Sie anschaulich, dass $\ \Theta$ eine Äquivalenzrelation ist. Formulieren Sie dazu die Eigenschaften von Äquivalenzrelationen konkret auf die Relation $\ \Theta$ bezogen.

Hinweis: Sie können die Transitivität noch nicht exakt beweisen; in dieser Aufgabe geht es zunächst darum, die Relationseigenschaften als geometrische Eigenschaften zu interpretieren und zu verstehen.

ich bleib bei dem anschaulichen canyon-beispiel:
reflexiv: wenn ich die strecke zwischen einem punkt der ebenen und genau den gleichen punkt nehme, wird die strecke ja nicht so wirklich lang und schafft es auf keinen fall, über die schlucht zu kommen--> ja, reflexiv
symmetrisch: wenn die strecke ab keine brücke über die schlucht spannt, macht es auch die strecke ba auch nicht--> ja, symmetrisch
transitiv: wenn die strecke zwischen a und b keine brücke bildet (sich auf einer seite der schlucht befindet) und die strecke bc keine brücke bildet (sich also ebenfalls auf der gleichen seite der schlucht befindet), dann kann auch die strecke ac keine brücke bilden-->ja, transitiv
fazit: äquivalenzrelation--Studentin 01:15, 11. Mai 2012 (CEST)