Übung Aufgaben 4 P (SoSe 12)
Inhaltsverzeichnis[Verbergen] |
Aufgaben zu Relationen und Äquivalenzklassen
Aufgabe 4.1
Entscheiden Sie für die folgenden Relationen, ob es sich um reflexive, symmetrische sowie transitive Relationen handelt?
- Parallelität von Geraden der Ebene
- Kongruenz geometrischer Figuren
- Teilbarkeit in

- Kleinerrelation in

- Größer-Gleich-Relation in

- Ungleichheit in

Lösung von Aufgabe 4.1P (SoSe_12)
Aufgabe 4.2
Untersuchen Sie folgende Relation S auf ihre Eigenschaften:
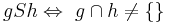
Lösung von Aufgabe 4.2P (SoSe_12)
Aufgabe 4.3
In der Schule sprechen wir davon, dass wir Dreiecke
a) hinsichtlich der Seitenlängen oder
b) hinsichtlich der Winkelgrößen klassifizieren.
In welchen der beiden Fälle handelt es sich um eine wirkliche Klasseneinteilung? Argumentieren Sie mit Hilfe eines Venn-Diagramms.
Lösung von Aufgabe 4.3P (SoSe_12)
Aufgabe 4.4
Gegeben sei eine Gerade g und ein Punkt P auf g. Durch diesen Punkt P wird die Gerade g in zwei Halbgeraden geteilt.
a) Warum ist diese Einteilung von g in die zwei Halbgeraden bezüglich P keine Klasseneinteilung auf der Menge der Punkte von g?
b) Geben Sie zwei Klasseneinteilungen auf der Menge der Punkte von g an, die den Punkt P und die auf g durch P bestimmten Halbgeraden in modifizierter Form verwenden.
Lösung von Aufgabe 4.4P (SoSe_12)
Aufgabe 4.5
Es seien eine Ebene E (aufgefasst als Punktmenge) und eine Gerade g in E gegeben. Wir betrachten folgende Relation  (
( ist ein willkürlich gewähltes Symbol, um die Relation nicht mit dem unauffälligen Buchstaben R bezeichnen zu müssen) in der Menge
ist ein willkürlich gewähltes Symbol, um die Relation nicht mit dem unauffälligen Buchstaben R bezeichnen zu müssen) in der Menge 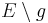 (also alle Punkte der Ebene E, die nicht der Geraden g angehören): Für beliebige
(also alle Punkte der Ebene E, die nicht der Geraden g angehören): Für beliebige 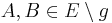 gilt:
gilt: 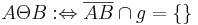 .
.
a) Beschreiben Sie die Relation  verbal und veranschaulichen Sie diese Relation.
verbal und veranschaulichen Sie diese Relation.
b) Begründen Sie anschaulich, dass  eine Äquivalenzrelation ist. Formulieren Sie dazu die Eigenschaften von Äquivalenzrelationen konkret auf die Relation
eine Äquivalenzrelation ist. Formulieren Sie dazu die Eigenschaften von Äquivalenzrelationen konkret auf die Relation  bezogen.
bezogen.
Hinweis: Sie können die Transitivität noch nicht exakt beweisen; in dieser Aufgabe geht es zunächst darum, die Relationseigenschaften als geometrische Eigenschaften zu interpretieren und zu verstehen.
Lösung von Aufgabe 4.5P (SoSe_12)
Aufgabe 4.6
Es sei 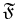 die Menge der Figuren der Ebene. Auf
die Menge der Figuren der Ebene. Auf 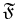 sei eine Äquivalenzrelation
sei eine Äquivalenzrelation  definiert.
definiert.  möge
möge 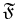 derart in Klassen einteilen, dass die folgenden Figuren in ein und derselben Klasse liegen:
derart in Klassen einteilen, dass die folgenden Figuren in ein und derselben Klasse liegen:
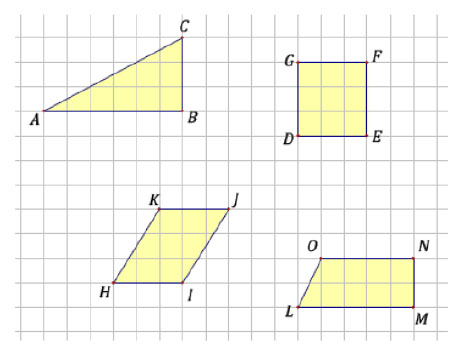
Geben Sie mögliche Interpretationen der Relation  an.
an.
Lösung von Aufgabe 4.6P (SoSe_12)

