Lösung von Aufgabe 5.5 (SoSe11)
Das Parallelenaxiom lautet wie folgt:
Zu jeder Geraden g und zu jedem nicht auf g liegenden Punkt A gibt es höchstens eine Gerade, die durch A verläuft und zu g parallel ist.
Nutzen Sie dieses Axiom, beim Lösen der folgenden Aufgabe:
Es seien a, b und c drei paarweise verschiedene Geraden in ein und derselben Ebene.
a) Beweisen Sie folgende Implikation durch einen Widerspruchsbeweis: 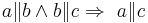 .
.
b) Welche Eigenschaft der Relation 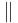 auf der Menge aller Geraden einer Ebene haben Sie hiermit gezeigt?
auf der Menge aller Geraden einer Ebene haben Sie hiermit gezeigt?
Ich mache mal einen Anfang:
Vor.: a, b und c sind drei paarweise versch. Geraden
Beh.: 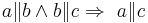 .
.
Annahme: 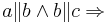
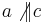
| Beweisschritt | Begründung |
| 1) a,b,c sind 3 paarweise versch. Geraden | Vor. |
| 2) es existiert ein Pkt A, der nicht auf der Geraden liegt (welche Gerade ist hier gemeint?) die Gerade a | Axiom I/0 |
| 3) durch A geht eine Gerade, die parallel zu a ist | 2), Parallelenaxiom |
| 4) eine weitere Gerade geht durch A und ist nicht parallel zu a (hm... ich verstehe die Beweisführung bzw. dieses Argument an dieser Stelle nicht und warum ist das ein Widerspruch zur Annahme? Vllt. wäre eine Skizze an dieser Stelle nicht schlecht.)--Tutor Andreas 13:42, 6. Mai 2011 (CEST)Und wie füge ich eine Skizze ein? Wie füge ich die ganzen mathematischen Zeichen ein? Ich habe nur von oben kopiert. --Flo 21 19:55, 8. Mai 2011 (CEST) | Def. Schnittpkt von Geraden |
| Widerspruch zur Vor. |
Voraussetzung: a, b, c sind paarweise verschiedene Geraden, 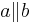 ,
, 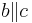
Behauptung: Annahme: 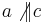
zu zeigen: b schneidet c, B ist Schnittpunkt der Geraden b und der Geraden c
| Nummer | Beweisschritt | Begründung |
| (1) | a, b, c sind paarweise verschiedene Geraden | Vor. |
| (2) | 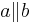 |
Vor. |
| (3) | 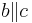 |
Vor. |
| (4) | B ε b | Festlegung, Schnittpunkt b, c |
| (5) | B ε c | Festlegung, Schnittpunkt b, c |
| (6) | b nicht parallel zu c | Parallelaxiom, (4), (5), Wiederspruch zur Annahme, dass 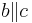 (du schreibst bei z.z., dass b die Gerade c schneidet. In diesem Beweisschritt erwähnst du, dass b nicht parallel zu c sein soll --> somit schneiden sie sich doch wieder und du hast keinen Widerspruch. Oder?)--Flo 21 20:15, 8. Mai 2011 (CEST) (du schreibst bei z.z., dass b die Gerade c schneidet. In diesem Beweisschritt erwähnst du, dass b nicht parallel zu c sein soll --> somit schneiden sie sich doch wieder und du hast keinen Widerspruch. Oder?)--Flo 21 20:15, 8. Mai 2011 (CEST)
|
So wie ich das sehe, hast du die Aufgabe nicht erfüllt. Der Beweis soll durch Widerspruch geführt werden. D.h. du benötigst erst die Vor. dann die Behauptung und dazu die Annahme. --Flo 21 20:15, 8. Mai 2011 (CEST)
somit wäre aus meiner sicht bewiesen, dass a auch parallel zu c ist. Falls dieser Beweis so stimmt:
Wie gehe ich mit folgenden Punkten um:
| Das hab ich geschrieben | das gefällt mir daran überhaupt nicht | so wäre es richtig |
| zu zeigen: b schneidet c, B ist Schnittpunkt der Geraden b und der Geraden c | das kann irgendwie nicht sein, weil das möchte ich eigentlich gar nicht zeigen. ich möchte vielmehr zeigen, dass a grad nicht parallel zu c ist, aber das ist ja meine Behauptung - irgendwie doppelt gemoppelt, oder? außerdem habe ich gar nicht gezeigt, dass b c schneidet (du solltest evtl vorab schreiben, dass sich 2 Geraden schneiden und dadurch ein Schnittpunkt entsteht. Eine Gerade ist in einem Axiom festgelegt, dass sie eine Menge von Punkten darstellt.) --Flo 21 20:15, 8. Mai 2011 (CEST) | |
| "Festlegung, Schnittpunkt b, c" in Beweisschritt 4 und 5 | ich glaube, dass man das irgendwie anders schreiben sollte - das scheint mir aber wenig professionell |
Dankeschön --Flo60 22:05, 7. Mai 2011 (CEST)
vielleicht ist aber auch das einfacher und bedeutend klüger:
Voraussetzung: a, b, c sind paarweise verschiedene Geraden, 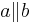 ,
, 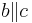
Behauptung: a schneidet c
zu zeigen: a ist nicht parralel zu b (bzw. b ist nicht parallel zu c)
| Nummer | Beweisschritt | Begründung |
| (1) | a, b, c sind paarweise verschiedene Geraden | Vor. |
| (2) | 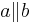 |
Vor. |
| (3) | 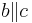 |
Vor. |
| (4) | A ε a | Schnittpunkt a, c |
| (5) | A ε c | Schnittpunkt a, c |
| (6) | a nicht parallel zu b | Parallelaxiom, (4), (5), Wiederspruch zur Annahme, dass 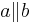
|
--Flo60 22:27, 7. Mai 2011 (CEST)
Dein zweite Variante ist m.E. überflüssig. Du führst den Beweis praktisch 2 Mal. Du kannst auch schreiben oBdA (ohne Beschränkung der Allgemeinheit) --Flo 21 20:15, 8. Mai 2011 (CEST)
Informiert euch über die Verwendung/ Bedeutung der Wörter Vorraussetzung, Behauptung, Annahme. In den vorrigen Beweisen wurden die falschen Dinge damit bezeichnet und auch deshalb klappten die Beweise nicht bzw. sie sind nicht korrekt. Unten folgt noch ein guter Ansatz.--Tutorin Anne 21:00, 13. Mai 2011 (CEST)
b) Wenn eine Gerade a parallel zu einer Gerade b ist und eine Gerade b zu einer Geraden c pparallel ist, dann ist auch eine Gerade a zu einer Geraden c parallel. Durch das "und" wird deutlich, dass beide Teilaussagen wahr sein müssen, damit die Gesamtaussage wahr wird. --Flo 21 15:30, 5. Mai 2011 (CEST)
Diese Eigenschaft, dass wenn a zu b und b zu c in Relation steht dann auch a zu c in Relation stehtnennt man Transitivität.Klemens 19:36, 5. Mai 2011 (CEST)
Meine Lösung zu a) sieht so aus: Nach der Vorraussetzung (besser: Annahme)schneiden sich die Geraden a und c in einem beliebigen Punkt A. Die Gerade b jedoch ist parallel zu a und zu c. Nach dem Parallelenaxiom gibt es aber in A höchstens eine Gerade die parallel zu b ist. => Widerspruch.
Ist das verständlich?
-->Ja ich finde das ist verständlich und würde sagen es ist auch richtig.
Müsste man dann als das zu zeigen folgendes schreiben: Es ist zu zeigen, dass es nur eine Gerade gibt, die parallel zu b verläuft und durch A geht? ...könnte jemand diesen letzten Gedanken nochmal in Tabellenform schreiben?--Fledermaus 22:53, 10. Mai 2011 (CEST)
Ja, versucht doch diese Idee noch in einer Tabelle festzuhalten:--Tutorin Anne 20:51, 13. Mai 2011 (CEST)
Voraussetzung: a, b, c sind paarweise verschiedene Geraden, 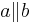 ,
, 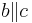
Behauptung: 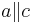
Annahme: 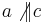
| Nummer | Beweisschritt | Begründung |
| (1) | 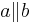 |
Vor |
| (2) | 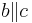 |
Vor |
| (3) | A ε a, A ε c | Annahme |
| (4) | a = c | Euklid. Parallelenaxiom ; Widerspruch: a,b,c paarweise verschieden |
--Hallelli 18:59, 4. Jun. 2011 (CEST) Gut! Besser ist allerdings noch, wenn man genauer begründet. Was ist A? Aus welchen Schritten folgt (4)?--Tutorin Anne 12:10, 6. Jun. 2011 (CEST)
.........................................................
ist das so richtig?
Voraussetzung: a,b,c paarweise verschieden, a ║ b, c ║ b
Behauptung: a ║ c
Annahme: a ⌐║c
BEWEIS:
| Nummer | Beweisschritt | Begründung |
| 1 | c ∩ a ={S}, also S ϵ a, S ϵ c | Annahme |
| 2 | a ║ b, c ║ b | Voraussetzung |
| 3 | a ≡ c | Schritt 1 und 2, Parallelenaxiom
Widerspruch zu Voraussetzung: a,b,c paarweise verschieden |
--...s... 13:25, 17. Jun. 2011 (CEST)
Gut!--Tutorin Anne 10:37, 18. Jun. 2011 (CEST)

