Aufgaben zu Sätzen und Beweisen Teil 2
Aufgabe 3.1
Referendarin Lisa muss den Satz über die Innenwinkelsumme im Dreieck mit ihrer 7b behandeln. In die fachlichen Vorbetrachtungen zur entsprechenden Einführungsstunde will sie den Satz auch in der Wenn-Dann-Form aufnehmen. Sie formuliert:
Satz: Wenn ein Dreieck drei Ecken hat, dann haben die Innenwinkel 180°.
(a) Warum ist die obige Formulierung des Innenwinkelsatzes nicht korrekt?
(b) Geben Sie eine korrekte Formulierung des Innenwinkelsatzes in der Wenn-Dann_form an.
Lösung von Aufgabe 3.1 WS_12_13
Aufgabe 3.2
Zur Erarbeitung des Satzes hat Lisa eine Geogebra-App erstellt:
Die Schüler generieren durch Ziehen an den Eckpunkten verschiedene Dreiecke und stellen fest, dass die Innenwinkelsumme immer 180° beträgt.
Danach formulieren sie den Innenwinkelsatz für Dreiecke. Lisa möchte dann mit den Schülern den Satz beweisen. Ihre Schüler sehen das nicht ein, die App wäre ja Beweis genug. Helfen Sie Lisa.
Lösung von Aufgabe 3.2 WS_12_13
Aufgabe 3.3
Mit Ihrer Hilfe hat es Lisa geschafft, die 7b von der Notwendigkeit eines korrekten Beweises des Innenwinkelsatzes zu überzeugen. Für den Beweis selbst wählt sie die bekannte enaktive Variante:
Die Schüler erhalten die Aufgabe eine beliebiges Dreieck zu zeichnen und abschließend auszuschneiden. Dann reißen sie die "Winkel"  und und  ab. Die abgerissenen Winkel werden abschließend an den Winkel ab. Die abgerissenen Winkel werden abschließend an den Winkel  derart angelegt, dass ein gestreckter Winkel entsteht. Die Innenwinkelsumme des Dreiecks muss also 180° betragen. (s. Flash-App) derart angelegt, dass ein gestreckter Winkel entsteht. Die Innenwinkelsumme des Dreiecks muss also 180° betragen. (s. Flash-App)
[ www.ph-heidelberg.de is not an authorized iframe site ]
Bei aller Sympatie für die Idee der enaktiven Beweisführung, der Beweis ist nicht korrekt. Warum nicht?
Lösung von Aufgabe 3.3 WS_12_13
Aufgabe 3.4
Wir stellen den enaktiven "Beweis" vom Kopf auf die Füße:
Satz (*): Es sei  ein Dreieck. ein Dreieck.
Wenn die Winkelpaare 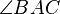 und und 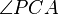 bzw. bzw.  und und 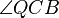 jeweils zueinander kongruente Wechselwinkel sind, jeweils zueinander kongruente Wechselwinkel sind,
dann gehören die Punkte 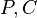 und und  ein und derselben Geraden an. ein und derselben Geraden an.
Führen Sie einen Widerspruchsbeweis für Satz (*).
Hilfe: Es gelten die folgenden Aussagen:
- Umkehrung des Wechselwinkelsatzes: Wenn beim Schnitt zweier Geraden
 und und  durch eine dritte Gerade durch eine dritte Gerade  kongruente Wechselwinkel entstehen, dann sind kongruente Wechselwinkel entstehen, dann sind  und und  zueinander parallel. zueinander parallel.
- Euklidisches Parallelenaxiom: (alles in der Ebene) Durch einen Punkt
 außerhalb der Geraden außerhalb der Geraden  gibt es höchsten eine Parallele zu gibt es höchsten eine Parallele zu  . .
Lösung von Aufgabe 3.4 WS_12_13
Aufgabe 3.5
Es gilt der Satz (IWSV): In jedem Viereck beträgt die Summe der Größen der Innenwinkel 360°.
Formulieren Sie die Kontraposition von Satz (IWSV)
Lösung von Aufgabe 3.5 WS_12_13
Aufgabe 3.6
Satz: In einem Dreieck  mit |AC|< |BC| < |AB| sind die Winkel α und β nicht kongruent zueinander. mit |AC|< |BC| < |AB| sind die Winkel α und β nicht kongruent zueinander.
a) Welcher Beweis ist korrekt? Begründen Sie ausführlich! (Der Basiswinkelsatz und seine Umkehrung seien bereits bewiesen.)
Beweis 1)
Sei  ein Dreieck. ein Dreieck.
Vor: |AC|< |BC| < |AB|.
Beh: |α| ≠ |β|
Bew: Da nach Voraussetzung |AC| ≠ |BC| gilt nach dem Basiswinkelsatz |α| ≠ |β|. Damit ist der Satz bewiesen.
Beweis 2)
Sei  ein Dreieck. ein Dreieck.
Vor: |AC|< |BC| < |AB|.
Beh: |α| ≠ |β|
Bew: Nach Umkehrung des Basiswinkelsatzes gilt: Wenn |α|= |β| dann gilt |AC|= |BC|. Die Kontraposition der Umkehrung lautet also: Wenn |AC| ≠ |BC| dann gilt |α| ≠ |β|. Da die Kontraposition gleichwertig ist, kann man auch diese beweisen. Da nach Voraussetzung gilt: |AC|< |BC|, d.h. |AC| ≠ |BC|, kann nach Kontraposition der Umkehrung des Basiswinkelsatzes direkt gefolgert werden: |α| ≠ |β|. Damit ist der Satz bewiesen.
b) Beweisen Sie den Satz indirekt mit Widerspruch.
Lösung von Aufgabe 3.6 WS_12_13
|  und
und  ab. Die abgerissenen Winkel werden abschließend an den Winkel
ab. Die abgerissenen Winkel werden abschließend an den Winkel  derart angelegt, dass ein gestreckter Winkel entsteht. Die Innenwinkelsumme des Dreiecks muss also 180° betragen. (s. Flash-App)
derart angelegt, dass ein gestreckter Winkel entsteht. Die Innenwinkelsumme des Dreiecks muss also 180° betragen. (s. Flash-App) ein Dreieck.
ein Dreieck. 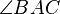 und
und 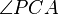 bzw.
bzw.  und
und 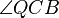 jeweils zueinander kongruente Wechselwinkel sind,
jeweils zueinander kongruente Wechselwinkel sind, 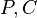 und
und  ein und derselben Geraden an.
ein und derselben Geraden an.
 und
und  durch eine dritte Gerade
durch eine dritte Gerade  kongruente Wechselwinkel entstehen, dann sind
kongruente Wechselwinkel entstehen, dann sind  außerhalb der Geraden
außerhalb der Geraden  gibt es höchsten eine Parallele zu
gibt es höchsten eine Parallele zu 
