Winkel, Innere eines Winkels, Nebenwinkel, Scheitelwinkel WS 11/12
Inhaltsverzeichnis[Verbergen] |
Winkel
Übungsblatt
Videos
Begriff des Winkels
Identifizieren von Winkeln
Repräsentanten und Gegenrepräsentanten
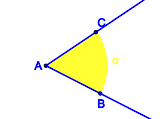
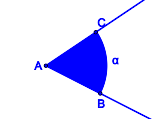
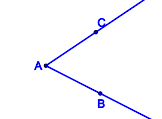
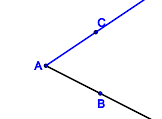
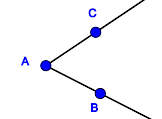
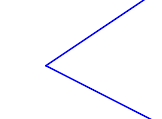
In welchen Fällen sind die jeweils blau gefärbten Punktmengen Modelle für Winkel?
 |
 |
 |
|
| Punktmenge 1 | Punktmenge 2 | Punktmenge 3 | Punktmenge 4 |
 |
 |
 |
|
| Punktmenge 5 | Punktmenge 6 | Punktmenge 7 | Punktmenge 8 |
Tabelle 1
| Winkelmodell | kein Winkelmodell |
|---|---|
| Punktmenge: |
Punktmenge: |
Prozess der Begriffserarbeitung als Generierung einer Klasseneinteilung
In der Didaktik bezeichnen wir die Art und Weise der Erarbeitung eines neuen Begriffs entsprechend obiger Tabelle als induktive Begriffserarbeitung: Eine gewisse Menge an Repräsentanten und Gegenrepräsentanten bezüglich des zu erarbeitenden Begriffs wird vorgegeben. Dann teilt man diese Menge in genau zwei Klassen ein. Die eine Klasse bilden alle Begriffsrepräsentanten, die andere Menge der Rest.
Aufgabe: Ergänzen Sie Tabelle 1 durch weitere Repräsentanten bzw. Gegenrepräsentanten zur Erarbeitung des Winkelbegriffs.
Zum besseren Verständnis: Analoge Erarbeitung des Begriffs Trapez:
Realisieren von Winkeln
Die Idee des konstruktiven Begriffserwerbs
Während beim induktiven Begriffserwerb das Ausgangsmaterial für den Schüler bereits vorgefertigt wurde, generiert er es sich beim konstruktiven Begriffserwerb selbst. Der gute Lehrer läßt in der Regel beide Varianten zur Anwendung kommen.
Konstruktion eines Winkels
Aufgabe: Zeichne einen Winkel
Lösung:
Definition des Winkelbegriffs
Definition V.1: (Winkel)
Unter einem Winkel 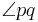 verseht man die Vereinigungsmenge der beiden Stahlen p und q mit dem gemeinsamen Scheitelpunkt S.
Fehler beim Parsen(Syntaxfehler): \angle pq:= \left\{ {\\ SP^{+} } \right\} \cup \left\{ {\ SQ^{+} } \right\}
--RicRic 22:59, 12. Dez. 2011 (CET)
verseht man die Vereinigungsmenge der beiden Stahlen p und q mit dem gemeinsamen Scheitelpunkt S.
Fehler beim Parsen(Syntaxfehler): \angle pq:= \left\{ {\\ SP^{+} } \right\} \cup \left\{ {\ SQ^{+} } \right\}
--RicRic 22:59, 12. Dez. 2011 (CET)
Arten, Winkel zu beschreiben
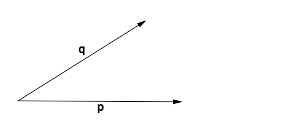
| Beispiel | Beschreibung | in Zeichen | Quelltext in Tex |
|---|---|---|---|
|
Winkel, der aus den beiden Strahlen  und und 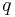 besteht. besteht.
|
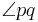
|
\angle pq |
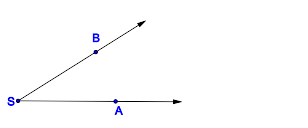
|
Winkel, der aus den beiden Strahlen 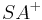 und und 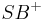 besteht. besteht.
|

|
\angle ASB |
Die Idee des gerichteten Winkels
Gerichtete Winkel werden in der Einführung in die Geometrie keine Rolle spielen. Trotzdem dürfen Sie hier ergänzen, was denn ein gerichtetet Winkel wäre.
Das Innere eines Winkels
So ist es zu verstehen
[ www.ph-heidelberg.de is not an authorized iframe site ]
Klicken Sie auf die Steuerknöpfe um die Halbebenen ein- und auszublenden.
da sieht man mal wieder, dass viele mathematiker keine künstlerisch-malerische seite besitzen....grün und blau gibt doch nicht rot :-P
Definition des Inneren eines Winkels
Definition V.2: (Inneres eines Winkels)
Unter dem Inneren eines Winkels  versteht man die Schnittmenge der beiden Halbebenen
versteht man die Schnittmenge der beiden Halbebenen 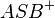 und
und 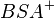 --RicRic 23:03, 12. Dez. 2011 (CET)
--RicRic 23:03, 12. Dez. 2011 (CET)
Satz V.1
- Das Innere eines Winkels ist konvex.
Beweis von Satz V.1
- trivial entsprechend Satz IV., Satz IV.3 und der Definition V.2
Überstumpfe Winkel?
Bemerkung: Entsprechend Definition V.2 beinhaltet unsere Geometrie keine überstumpfen Winkel.
Scheitelwinkel und Nebenwinkel
Scheitelwinkel
Beispiele und Gegenbeispiele
Definition
Definition V.3: (Scheitelwinkel)
Def.1: Scheitelwinkel sind zwei Winkel, deren Schenkel vereinigt je eine Gerade bilden.
Def.2: Zwei Winkel sind Scheitelwinkel, wenn ihre Schenkel zwei sich schneidende Geraden bilden.--RicRic 23:11, 12. Dez. 2011 (CET)
- Was heißt denn "Schenkel bilden eine Gerade"? --Spannagel 14:01, 6. Jan. 2012 (CET)
- Die Vereinigungsmenge der Punktmenge von zwei Schenkeln ergibt die Menge einer Gerade. --RicRic 19:35, 6. Jan. 2012 (CET)
Eine kure Frage: Darf man dann nicht einfach "..., wenn jeweils ein Schenkel von < ASB mit einem Schenkel von < CSD EINE GERADE BILDEN" schreiben?
und ist diese Definition okay: "Zwei Winkel < ASB und < CSD sind Scheitelwinkel, wenn die Vereinigungsmenge der Punktmengen von jeweils einem Schenkel von < ASB mit genau einem Schenkel von < CSD die Menge aller Punkte einer Geraden ergeben." --Geogeo12 19:14, 11. Jan. 2012 (CET)
Nebenwinkel
Beispiele und Gegenbeispiele
Definition
Definition V.4: (Nebenwinkel)
zwei Winkel sind Nebenwinkel, wenn sie einen identischen Schenkel haben und der jeweils andere Schenkel dieser Winkel eine Gerade bildet.--RicRic 23:13, 12. Dez. 2011 (CET)