Zusatzaufgaben 2 (SoSe 16)
Aus Geometrie-Wiki
Inhaltsverzeichnis |
Aufgabe 2.1
Definieren Sie den Begriff gleichschenkliges Trapez. Beachten Sie dabei, dass ein Parallelogramm dann und nur dann ein gleichschenkliges Trapez ist, wenn es einen rechten Innenwinkel besitzt.
Lösung von Zusatzaufgabe 2.1P (SoSe_16)
Aufgabe 2.2
Ein Tangentenviereck ist das, was der Begriff suggeriert. Definieren Sie den Begriff Tangentenviereck
Lösung von Zusatzaufgabe 2.2P (SoSe_16)
Aufgabe 2.3
Begründen Sie, dass es sinnvoll ist, den Begriff Tangentenviereck zu definieren.
Lösung von Zusatzaufgabe 2.3P (SoSe_16)
Aufgabe 2.4
Peter möchte den Begriff Tangentendreieck definieren. Kommentieren Sie dieses Unterfangen.
Lösung von Zusatzaufgabe 2.4P (SoSe_16)
Aufgabe 2.5
Welche Definition für Kreis ist richtig? Warum (nicht)?
- Sei
 ein Punkt und
ein Punkt und  eine Menge, deren Elemente Punkte sind. Wenn gilt:
eine Menge, deren Elemente Punkte sind. Wenn gilt:  ist konstant, so ist
ist konstant, so ist  ein Kreis mit Mittelpunkt
ein Kreis mit Mittelpunkt  .
.
- Sei
 ein Punkt und
ein Punkt und  eine Punktmenge. Wenn gilt:
eine Punktmenge. Wenn gilt: 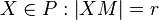 , dann ist
, dann ist  ein Kreis.
ein Kreis.
- Sei
 ein Punkt in der Ebene
ein Punkt in der Ebene  und
und  eine Punktmenge. Wenn
eine Punktmenge. Wenn  alle Punkte
alle Punkte 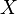 enthält für die gilt∶
enthält für die gilt∶  und
und 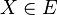 , dann ist
, dann ist  ein Kreis mit dem Mittelpunkt
ein Kreis mit dem Mittelpunkt  .
.
- Sei
 ein Punkt in der Ebene
ein Punkt in der Ebene  und
und  eine Punktmenge. Wenn
eine Punktmenge. Wenn  genau alle Punkte
genau alle Punkte 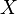 enthält für die gilt∶
enthält für die gilt∶  und
und 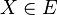 , dann ist
, dann ist  ein Kreis mit dem Mittelpunkt
ein Kreis mit dem Mittelpunkt  .
.
- Sei
 ein Punkt in der Ebene
ein Punkt in der Ebene  und
und  eine Menge, deren Elemente Punkte sind. Wenn für alle
eine Menge, deren Elemente Punkte sind. Wenn für alle 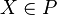 gilt∶
gilt∶  , dann ist
, dann ist  ein Kreis.
ein Kreis.
- Sei
 ein Punkt und
ein Punkt und  eine Menge, deren Elemente Punkte sind. Alle Elemente von
eine Menge, deren Elemente Punkte sind. Alle Elemente von  liegen in ein und derselben Ebene wie
liegen in ein und derselben Ebene wie  . Wenn gilt:
. Wenn gilt:  ist konstant, so ist
ist konstant, so ist  ein Kreis mit Mittelpunkt
ein Kreis mit Mittelpunkt  .
.

