Lösung von Aufg. 11.7 (WS 11/12): Unterschied zwischen den Versionen

Version vom 4. Januar 2012, 12:21 Uhr

Beweisen Sie die Gültigkeit der Umkehrung des Basiswinkelsatzes

Vorr.: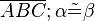 $\overline{ABC} ; \alpha \tilde {=} \beta$

Beh.: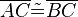 $\overline{AC} \tilde {=} \overline{BC}$

Beweis:

Schritt	Begründung
(1)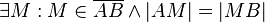 $\exists M:M\in \overline{AB} \wedge \left\| AM \right\| =\left\| MB \right\|$	Existenz und Eindeutigkeit des Mittelpunktes
(2) 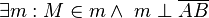$\exists m:M\in m \wedge \ m \perp \overline{AB}$	Existenz und Eindeutigkeit der Mittelsenkrechten, (1)
(3) zu Zeigen: 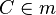$C\in m$	Dann gilt die Behauptung, Satz. Jeder Punkt vom m hat den selben Abstand zu A und B
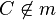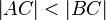(4) Ann.: $C\not\in m$ d.h. o.B.d.A. $\left\| AC \right\| < \left\| BC \right\|$
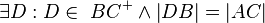(5) $\exists D: D\in \ BC^{+} \wedge \left\| DB \right\| = \left\| AC \right\|$	Axiom vom Lineal, Abstandsaxiom, (4)
(6) C im inneren von 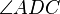$\angle ADC$	Winkeladditonsaxiom (5)
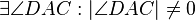(7) $\exists \angle DAC : \|\angle DAC\| \neq 0$	(4),(5),(6)
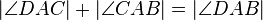(8) $\|\angle DAC\| + \|\angle CAB\| = \|\angle DAB\|$	(5),(6),(7) Winkeladditonsaxiom
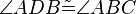(9) $\angle ADB \tilde {=} \angle ABC$	Basiswinkelsatz (5)
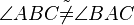(10) $\angle ABC \tilde \neq \angle BAC$ Wiederspruch zur Vorr., Annahme verwerfen, Behaupt stimmt	(9),(8),(7),(5)

--RicRic 13:04, 3. Jan. 2012 (CET)

@@ Zeile 25: / Zeile 25: @@
 |  (7) <math>\exists \angle DAC : |\angle DAC| \neq 0</math> || (4),(5),(6)
 |-
-|  (8) <math>|\angle DAC| + |\angle CAB|  = |\angle DAB|</math>  || (5),(6),(7) Winkeladditonsaxiom
+|  (8) <math>|\angle DAC| + |\angle CAB|  = |\angle DAB|</math> || (5),(6),(7) Winkeladditonsaxiom
 |-
-|  (9) <math>\angle ADB \tilde {=} \beta   \angle ABC</math>  || Basiswinkelsatz (5)
+|  (9) <math>\angle ADB \tilde {=}    \angle ABC</math>  || Basiswinkelsatz (5)
 |-
-|   (10)<math>\angle ABC  nicht \tilde {=} \angle BAC </math>  Wiederspruch zur Vorr., Annahme verwerfen, Behaupt stimmt  || (9),(8),(7),(5)
+|   (10)<math>\angle ABC  \tilde \neq \angle BAC </math>  Wiederspruch zur Vorr., Annahme verwerfen, Behaupt stimmt  || (9),(8),(7),(5)
 |}--[[Benutzer:RicRic|RicRic]] 13:04, 3. Jan. 2012 (CET)
 <ggb_applet width="784" height="484"  version="4.0" ggbBase64="UEsDBBQACAAIAHJoI0AAAAAAAAAAAAAAAAAWAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc0srzUsuyczPU0hPT/LP88zLLNHQVKiuBQBQSwcI1je9uRkAAAAXAAAAUEsDBBQACAAIAHJoI0AAAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1s7VlZb9s4EH5ufwWh51gmddkunBZNi2ILJG2x6S4W+0ZJtMxGFrUifRX98TskJVmynatNi2SxRmxeQw7nm1PK9NVmkaMVqyQXxalDXOwgViQi5UV26izVbDB2Xr18Ps2YyFhcUTQT1YKqUyfQlDw9dbA3CjyaTAYx9meDwEvjwThIRoPJLCU4Yn40iaiD0EbyF4X4QBdMljRhl8mcLei5SKgyjOdKlS+Gw/V67TasXFFlwyyL3Y1MHQTXLOSpU3dewHG9TWvfkHsYk+FfF+f2+AEvpKJFwhykRVjyl8+fTde8SMUarXmq5qfOGIMYc8azOcgU6cFQE5UASMkSxVdMwtbO0MisFqVjyGih15/ZHspbcRyU8hVPWQX4uF7oIFFxVqh6ldRchs3+6YqztT1I9wyPwEFKiDym+gz07RvysIfRiW6IbTxoosguYTuHfdt4tglsE1qawG4PLGlgaQJLE/gOWnHJ45ydOjOaS8CMF7MK9NWOpdrmzNynntjJS05AJsm/ArGvQbQgwzzGJ/oLyJ4EDbodIUmHq6qW92TasByNg7uz9H5IUL/h6R0T0wuvETO6gamV+y5ykrDDE1iZP/M94OjfJOY+Rzv+MYZR8EtEnA4bV5nW3oHkXNPW1qPYQhp/QYH+Ifo70T/gA8jTHT3t63X46kkCHoQiPRrppdBsGWkiveAbcg/V3HlRLlXNsRYiWaQNdyXKdhrIwb93ccP6ey+sPJvmNGY5RNpLjQxCK5pr+zScZqJQqLU1O5dVtJzzRF4ypWCXRF/oip5TxTbvgFo2vA1tIgr5qRLqjciXi0IilIgcNxeFPun0vZ0wIvc7C0F3IewsRJ3+6ChfAStoKRnwF5VsyGmavtcUO1cDKD8W+fasYvSqFLwvxnRogvaULZOcp5wWf4LyNReNC2piuHH/JoYHYdRcRFTp5VaCRaDN36wSgCMJddba2pGvR90POKlMqLbfEBu6zqj7IZYBW7V6oBu2EymrtD90Bu/lmch3U0bKN7RUy8okWQgplb776yLLmbEEE6QggyVXsdhcWr/w7VmftyWManuIM4MuAo/yQkgyWd3GtjU0+motFTY02FC0NsXTdp1MPENh2ti2hgqM1F6tFpU0YhLcsOHSlgNO3z2MieuEuCy4Om8GiidXtajEbviwXMSsNZT+meShzpwO9yxpesWqguW14YIyl2IprR92bDplCV/A0C40Emt1/QEXsLMpyyrWXDw3BYwFrLvH2uTBtDnqXSUW74vVZ7CFvQtMh80tpzKpeKltDsUQPK/YzqpSLinE3rS7T3saiJ7oGAvwKA0N+OBSzUVlahQIHdBqB8vZAuoTpIx5GQttYX5tSh2NJxLxF4hebcKw6zuFwfJRUzNGSfNyTnU5VAud0y2rejCY8y5Eug8OYG8kAFcurW5LxqxZ2PtCp4TjjDf1QhGgLdFGM43AoLe6vh056Kutc22hp0XVLmZ5Bt3ZPT2B8ViUbsHrzdPHy3N9i1fgjryfDtjZ0wcscKOxAcxzyfhBAEvEYkGLFBWmgPok8m0mCmdXg1CsPRNRog0OUU/DaDFaqmYdYlwOSYRYssSSwcMYhRwfW4Y1myMasgwbHbRH9bOBgnLkCp5hpEljqk5OpvMbT1NmSrvhzertANrVLwl9o+GQ1Olqp2ByHwVfb4WSZXrUXiS5xQ7vf9F7WuLOnga+i8mk+4nq+BX1Zic2nA3A2sgo7MyP9/P23TXF/insFmmTKV+UOU+4as0r147wvlCQWpnJLYcZ84qxUpcqH4vPFS2kfmlgaTqZ+I5aoY9HK54b+keUAtEyqtUwcrFPegT/FTXEj0cN2A3GvYLc5qpB4GKrh8iNcNDV1BPSQj/uX/DU5sqjgf8w4l/cFtW7effiu/KuftDPbBPb5iEcKwrr+DYJfkL6/FhByQvpjObnYAN7YF5YMOMDMNObwdTm1GKVfp979B/IHgBJ6wPb405iQpROIb3c8nOc43pl/E63exo4a+qYfQ2wmzVQwUkNwOyRKGBwTZIYtFniSSeJ/bL0MDaxAy2+vU9QevtdQYl49vWHaR/DAwF4mR9OAp9EIzwiIY6sFYRuEEaej6NwQqLxGD/Mw1VfKZd15j6aMt4eaGd2s3b264DZY/Ez3x31oCSjOoNg0gPe5hMMJYGukCMviCIfT8KnVCDfFj+v1W129/iZ/a/XX67XYfcFnXnbXf/r8+W/UEsHCBBvDRN7BgAAlx0AAFBLAQIUABQACAAIAHJoI0DWN725GQAAABcAAAAWAAAAAAAAAAAAAAAAAAAAAABnZW9nZWJyYV9qYXZhc2NyaXB0LmpzUEsBAhQAFAAIAAgAcmgjQBBvDRN7BgAAlx0AAAwAAAAAAAAAAAAAAAAAXQAAAGdlb2dlYnJhLnhtbFBLBQYAAAAAAgACAH4AAAASBwAAAAA=" framePossible = "false" showResetIcon = "false" showAnimationButton = "true" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" useBrowserForJS = "true" allowRescaling = "false" />

Lösung von Aufg. 11.7 (WS 11/12): Unterschied zwischen den Versionen

Version vom 4. Januar 2012, 12:21 Uhr

Navigationsmenü

Meine Werkzeuge

Namensräume

Varianten

Ansichten

Aktionen

Suche

Navigation

Werkzeuge