Lösung von Aufg. 11.7 (WS 11/12)
Beweisen Sie die Gültigkeit der Umkehrung des Basiswinkelsatzes
Vorr.: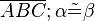
Beh.: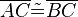
Beweis:
| Schritt | Begründung |
|---|---|
(1)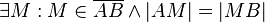 |
Existenz und Eindeutigkeit des Mittelpunktes |
(2) 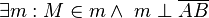 |
Existenz und Eindeutigkeit der Mittelsenkrechten, (1) |
(3) zu Zeigen: 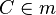 |
Dann gilt die Behauptung, Satz. Jeder Punkt vom m hat den selben Abstand zu A und B |
(4) Ann.: 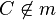 d.h. o.B.d.A. d.h. o.B.d.A. 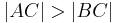 |
|
(5) 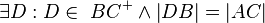 wenn man an dieser Stelle annimt, dass hier ein gleichschenkliges Dreieck entsteht, so setzt man ja schon voraus, dass der Punkt D und der Punkt C identisch sind... --Tutor Andreas 14:16, 16. Jan. 2012 (CET) wenn man an dieser Stelle annimt, dass hier ein gleichschenkliges Dreieck entsteht, so setzt man ja schon voraus, dass der Punkt D und der Punkt C identisch sind... --Tutor Andreas 14:16, 16. Jan. 2012 (CET) |
Axiom vom Lineal, Abstandsaxiom, (4) |
(6) C im inneren von 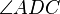 C im inneren von 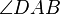 --RicRic 14:12, 5. Jan. 2012 (CET) --RicRic 14:12, 5. Jan. 2012 (CET) |
Winkeladditonsaxiom (5) |
(7) 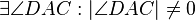 |
(4),(5),(6) |
(8) 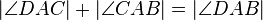 |
(5),(6),(7) Winkeladditonsaxiom |
(9) Fehler beim Parsen(Syntaxfehler): \angle ADB \tilde
(meinst du hier den Winkel 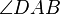 --Tutor Andreas 08:39, 12. Jan. 2012 (CET)) --Tutor Andreas 08:39, 12. Jan. 2012 (CET)) 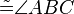 |
Basiswinkelsatz (5) |
(10)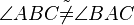 Wiederspruch zur Vorr., Annahme verwerfen, Behaupt stimmt Wiederspruch zur Vorr., Annahme verwerfen, Behaupt stimmt |
(9),(8),(7),(5) |
Also ich habe mir den Beweis jetzt mehrmals durchgeschaut, aber irgendwie passt da etwas nicht... die Begründung von Schritt 9 durch den Basiswinkelsatz und Schritt 5 kann ich nicht nachvollziehen, denn woher weiß man, dass 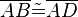 gilt?--Tutor Andreas 12:35, 4. Jan. 2012 (CET)Danke--RicRic 14:12, 5. Jan. 2012 (CET)
gilt?--Tutor Andreas 12:35, 4. Jan. 2012 (CET)Danke--RicRic 14:12, 5. Jan. 2012 (CET)
Ich schreibe doch gar nicht, dass die Strecken 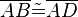 kongruent sind. Ich betrachte die Mittelsenktrechte der Strecke
kongruent sind. Ich betrachte die Mittelsenktrechte der Strecke  und sage, dass die eine Seite o.B.d.A. länger ist als die andere Seite, dann trage ich die längere Seite auf dem Strahl der kürzeren an und habe somit ein gleichschenkliges Dreieck, bei dem die Basiswinkel kongruent sind, stelle dann fest, dass der eine Basiswikel aber größer ist als der andere von meinem ursprünglichen Dreieck, somit komme ich zu dem Wiederspruch und sage die Stecken müssen also gleich lang sein bzw. C Element der Mittelsenkrechten von der Stecke AB. Ich hoffe mit ist es jetzt gelungen meine Beweisidee zu veranschaulichen. --RicRic 22:54, 4. Jan. 2012 (CET)
und sage, dass die eine Seite o.B.d.A. länger ist als die andere Seite, dann trage ich die längere Seite auf dem Strahl der kürzeren an und habe somit ein gleichschenkliges Dreieck, bei dem die Basiswinkel kongruent sind, stelle dann fest, dass der eine Basiswikel aber größer ist als der andere von meinem ursprünglichen Dreieck, somit komme ich zu dem Wiederspruch und sage die Stecken müssen also gleich lang sein bzw. C Element der Mittelsenkrechten von der Stecke AB. Ich hoffe mit ist es jetzt gelungen meine Beweisidee zu veranschaulichen. --RicRic 22:54, 4. Jan. 2012 (CET)
_______________________________________
Bis Schritt 8 ist mir alles klar, aber dann denke ich muss es so weiter gehn:
Vorr.: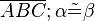
Beh.: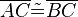
Beweis:
| Schritt | Begründung |
|---|---|
(1)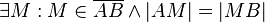 |
Existenz und Eindeutigkeit des Mittelpunktes |
(2) 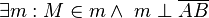 |
Existenz und Eindeutigkeit der Mittelsenkrechten, (1) |
(3) zu Zeigen: 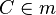 |
Dann gilt die Behauptung, Satz. Jeder Punkt vom m hat den selben Abstand zu A und B |
(4) Ann.: 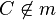 d.h. o.B.d.A. d.h. o.B.d.A. 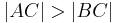 |
|
(5) 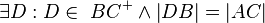 |
Axiom vom Lineal, Abstandsaxiom, (4) |
(6) C im inneren von 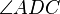 C im inneren von 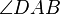 --RicRic 14:12, 5. Jan. 2012 (CET) --RicRic 14:12, 5. Jan. 2012 (CET) |
Winkeladditonsaxiom (5) |
(7) 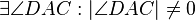 |
(4),(5),(6) |
(8) 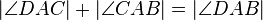 |
(5),(6),(7) Winkeladditonsaxiom |
(9) 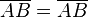 |
trivial |
(10) 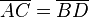 |
(5) |
(11) 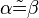 |
Vorr |
(12) 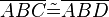 |
(9),(10),(11), SWS |
| (13) Fehler beim Parsen(Unbekannte Funktion „\lightning“): C = D \lightning zur Ann. | (12) |

