Serie 5 SoSe 2013: Unterschied zwischen den Versionen
*m.g.* (Diskussion | Beiträge) (→Aufgabe 5.01) |
*m.g.* (Diskussion | Beiträge) (→Aufgabe 5.01) |
||
| Zeile 16: | Zeile 16: | ||
Inzidenz <math>\operatorname{inz}</math>:<br /> Elementbeziehung: Ein Punkt <math>P</math> inzidiert mit einer Geraden <math>g</math> , wenn er zu <math>g</math> gehört: <math>P \operatorname{inz} g :\Leftrightarrow P \in g</math> | Inzidenz <math>\operatorname{inz}</math>:<br /> Elementbeziehung: Ein Punkt <math>P</math> inzidiert mit einer Geraden <math>g</math> , wenn er zu <math>g</math> gehört: <math>P \operatorname{inz} g :\Leftrightarrow P \in g</math> | ||
<br /><br /><br /> | <br /><br /><br /> | ||
| − | a) Warum ist | + | a) Warum ist <math>\mathbb{M}</math> kein Modell für die ebene Inzidenzgeometrie?<br /> |
| − | b) Ergänzen Sie | + | b) Ergänzen Sie <math>\mathbb{M}</math> derart, dass alle Axiome der ebenen Inzidenz erfüllt sind. |
<br /><br /> | <br /><br /> | ||
[[Lösung von Aufgabe 5.01 S SoSe 13]] | [[Lösung von Aufgabe 5.01 S SoSe 13]] | ||
Version vom 22. Mai 2013, 15:49 Uhr
|
Aufgabe 5.01Wir betrachten das folgende Modell Aufgabe 5.02Die Axiome eines Axiomensystems sollen unabhängig voneinander sein. Was versteht man darunter?
Aufgabe 5.03Die Axiome eines Axiomensystems sollen widerspruchsfrei sein. Was versteht man darunter?
Aufgabe 5.04Satz I: Je drei nicht kollineare Punkte sind paarweise verschieden.
Aufgabe 5.05Beweisen Sie Satz I.6: Eine Ebene und eine nicht in ihr liegende Gerade haben höchstens einen Punkt gemeinsam. Lösung von Aufgabe 5.05 S SoSe 13 Aufgabe 5.06Definieren Sie den Begriff der Komplanarität für Punkte. Ab wieviel Punkte macht der Begriff Sinn? Begründen Sie Ihre Antwort. Lösung von Aufgabe 5.06 S SoSe 13
Aufgabe 5.07Man muß jederzeit an Stelle von ‚Punkten‘, ‚Geraden‘, ‚Ebenen‘, ‚Tische‘, ‚Stühle‘, ‚Bierseidel‘ sagen können. Interpretieren Sie die Aussage von Hilbert bezüglich der axiomatischen Geometrie. Hinweis: Der Begriff des Modells hilft. Aufgabe 5.08Wir schreiben das Jahr 2022. Sie sind eine gestandene Mathematiklehrerin bzw. ein gestandener Mathematiklehrer. Das Blatt hat sich inzwischen gewendet und die Erleichterungspädagogik (Du magst keine Mathematik, dann sing doch ein Lied, du kannst kein Lied singen, dann bau doch einen Turm, du kannst keinen Turm bauen, dann streichle doch einen Esel, du traust dich nicht einen Esel zu streicheln, .. ist doch egal du bist so autistisch quatsch authentisch ... ) ist nicht mehr gesellschaftsfähig. Stattdessen haben Hardcoremathematiker aus China bezüglich des deutschen Mathematikunterrichts das Sagen. Die Lehrmittelverlage (die Pharmaindustrie der Bildung) freut sich und produziert neuen Content (hard und soft/ Hauptsache es bringt Geld). Ein Außendienstler von KlättKotza (Die Namenswahl ist zufällig und hat nichts mit existierenden Lehrmittelverlagen zu tun. Ähnlichkeiten sind auch nicht beabsichtigt.) erscheint bei Ihnen und möchte Ihnen einen Schülersatz Modelle für die räumliche Inzidenzgeometrie verkaufen:" Schauen Sie mal da hätten wir jeweils drei Flummis als Modellpunkte für die räumliche Inzidenzgeometrie, die können Sie dann auf diese 2 Schaschlikstäbchen, die Modellgeraden stecken. Schüler lieben Flummis und Schaschlik. Natürlich enthalten unsere Flummis krebserregende Weichmacher (da sind wir ganz ehrlich), die entweichen jedoch erst in 123 Jahren. Wenn Sie 10 Klassensätze kaufen, bekommen Sie den 12. umsonst und 10 Gratisexamplare von unserer Firmenzeitschrift Die Welt von KlättKotza."
Lösung von Aufgabe 5.08 S SoSe 13 Aufgabe 5.09Mario: Jede Gerade hat unendlich viele Punkte. Aufgabe 5.10Beweisen Sie: |
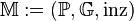für die Inzidenzgeometrie:
:
:
:
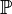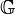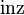inzidiert mit einer Geraden 
, wenn er zu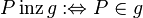 
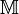kein Modell für die ebene Inzidenzgeometrie?
, 
und 
drei Punkte.“ Ergänzen Sie: „Wenn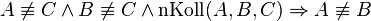 
.
