Übung Aufgaben 13 (WS 18 19): Unterschied zwischen den Versionen
Aus Geometrie-Wiki
(Die Seite wurde neu angelegt: „==Aufgabe 13.1== Zeigen Sie, dass bei der Verkettung einer Schubspiegelung <math>G_{a,b,c}</math> (<math>a \parallel b \wedge a \perp c</math>) mit einer Spieg…“) |
(→Aufgabe 13.3) |
||
| Zeile 18: | Zeile 18: | ||
==Aufgabe 13.3== | ==Aufgabe 13.3== | ||
Beweisen Sie die Umkehrung des Wechselwinkelsatzes mit abbildungsgeometrischen Methoden. Hinweis: Der Wechselwinkelsatz ist bereits bewiesen.<br /> | Beweisen Sie die Umkehrung des Wechselwinkelsatzes mit abbildungsgeometrischen Methoden. Hinweis: Der Wechselwinkelsatz ist bereits bewiesen.<br /> | ||
| − | [[Lösung von | + | [[Lösung von Aufgabe 13.3P (WS_18/19)]] |
| − | + | ||
==Aufgabe 13.4== | ==Aufgabe 13.4== | ||
Aktuelle Version vom 15. Januar 2019, 15:17 Uhr
Inhaltsverzeichnis |
Aufgabe 13.1
Zeigen Sie, dass bei der Verkettung einer Schubspiegelung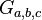 
(
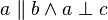) mit einer Spiegelung 
(
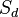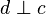) eine Punktspiegelung entsteht.
Lösung von Aufgabe 13.1P (WS_18/19)
Aufgabe 13.2
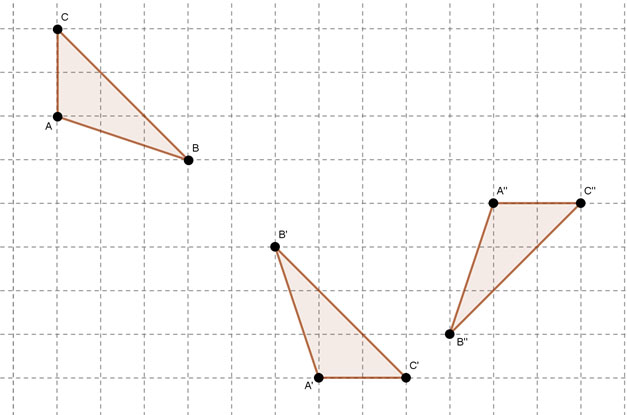
Dargestellt ist hier die Nacheinanderausführung zweier Abbildungen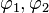 
, mit 
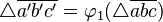und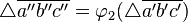 
.
- wie heißen die beiden Abbildungen
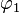und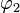 
?
- Zeichnen Sie jeweils für 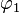und 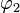die passende Anzahl von Spiegelachsen in die Skizze ein.
- Durch welche Ersatzabbildung kann die Verkettung
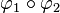ersetzt werden (Begründen Sie Ihre Entscheidung)?
- Zeichnen Sie die Achsen der Ersatzabbildung in die Skizze ein.
Lösung von Aufgabe 13.2P (WS_18/19)
Aufgabe 13.3
Beweisen Sie die Umkehrung des Wechselwinkelsatzes mit abbildungsgeometrischen Methoden. Hinweis: Der Wechselwinkelsatz ist bereits bewiesen.
Lösung von Aufgabe 13.3P (WS_18/19)
Aufgabe 13.4
Beweisen Sie den Innenwinkelsatz für Dreiecke mit Hilfe zweier Punktspiegelungen.
Lösung von Aufgabe 13.4P (WS_18/19)
