Verschiebungen 2010: Unterschied zwischen den Versionen
(→Satz: Jede Verschiebung ist eine Bewegung.) |
(→Satz: Jede Verschiebung ist eine Bewegung.) |
||
| Zeile 49: | Zeile 49: | ||
<br /><br /> | <br /><br /> | ||
| − | <br />Es sei <math>\ V</math> eine Verschiebung längs des Pfeiles <math>\overrightarrow{AB}</math> und <math>\ {P,Q}</math> zwei beliebige Punkte der Ebene mit ihren | + | <br />Es sei <math>\ V</math> eine Verschiebung längs des Pfeiles <math>\overrightarrow{AB}</math> und <math>\ {P,Q}</math> zwei beliebige Punkte der Ebene mit ihren Bildern <math>\ {P',Q'}</math> bei <math>\ V</math>, die voneinander verschieden sind und nicht auf dem Pfeil <math>\overrightarrow{AB}</math> liegen. |
<br /> | <br /> | ||
Wir haben zu zeigen, dass <math>\overline{PQ} \cong \overline {P'Q'}</math> ist. Es genügt natürlich zu zeigen, dass <math>\overline {PQQ'P'}</math> ein Parallelogramm ist, da in jedem Parllelogramm die gegenüberliegenden Seiten gleich lang sind. | Wir haben zu zeigen, dass <math>\overline{PQ} \cong \overline {P'Q'}</math> ist. Es genügt natürlich zu zeigen, dass <math>\overline {PQQ'P'}</math> ein Parallelogramm ist, da in jedem Parllelogramm die gegenüberliegenden Seiten gleich lang sind. | ||
Version vom 17. November 2010, 16:56 Uhr
Inhaltsverzeichnis[Verbergen] |
Konstruktion des Bildes eines Punkte bei einer Verschiebung
Unter Verwendung der Vektorrechnung (Pfeilklassen)
"Konstruktionsvorschrift": 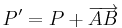
Konstruktionsbeschreibung
Gegeben sind ein Punkt 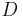 und sein Bildpunkt
und sein Bildpunkt 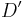 , sowie ein Punkt
, sowie ein Punkt  . Gesucht ist sein Bildpunkt
. Gesucht ist sein Bildpunkt  bei der Verschiebung an
bei der Verschiebung an 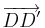
(1) Für den Fall, dass gilt: 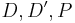 sind nicht kollinear.
sind nicht kollinear.
- 1. Parallele zu
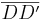 durch
durch 
- 1. Parallele zu
- 2. Parallele zu
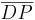 durch
durch 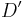
- 2. Parallele zu
- 3. Der Schnittpunkt der beiden zuvor konstruierten Parallelen ist der gesuchte Punkt

- 3. Der Schnittpunkt der beiden zuvor konstruierten Parallelen ist der gesuchte Punkt
(2) Für den Fall, dass gilt: 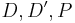 sind kollinear.
sind kollinear.
- 1. Konstruiere einen beliebigen Punkt
 der Ebene der nicht kollinear zu
der Ebene der nicht kollinear zu 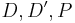 ist.
ist.
- 1. Konstruiere einen beliebigen Punkt
- 2. Konstruiere den Bildpunkt
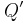 von
von  bei der Verschiebung an
bei der Verschiebung an 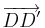 , wie in (1) beschrieben.
, wie in (1) beschrieben.
- 2. Konstruiere den Bildpunkt
- 3. Konstruiere nun den Bildpunkt
 von
von  bei der Verschiebung an
bei der Verschiebung an 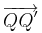 wie in (1) beschrieben.
wie in (1) beschrieben.  ist nun auch der gesuchte Bildpunkt für die Verschiebung an
ist nun auch der gesuchte Bildpunkt für die Verschiebung an 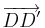 , da
, da 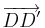 und
und 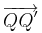 den gleichen Richtungssinn haben. --Steph85
den gleichen Richtungssinn haben. --Steph85
- 3. Konstruiere nun den Bildpunkt
Definition der Verschiebung
...
Eine andere Möglichkeit der Definition?
Es sei 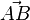 ein Pfeil. Unter der Verschiebung längs des Pfeiles
ein Pfeil. Unter der Verschiebung längs des Pfeiles 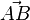 vresteht man eine Abbildung der Ebene auf sich, mit folgenden Eigenschaften:
vresteht man eine Abbildung der Ebene auf sich, mit folgenden Eigenschaften:
Für das Bild eines Punktes P, benannt mit P' muss gelten:
1. 
2. 
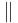
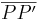
3. 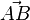 und
und 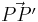 haben den selbern Richtungssinn
haben den selbern Richtungssinn
--Tja??? 17:23, 16. Nov. 2010 (UTC)
Sätze
Satz: Jede Verschiebung ist eine Bewegung.
An dieser Stelle wird nur der allgemeinste Fall bewiesen (siehe Skizze), da die Beweise der anderen Fälle laut Herr Gieding immer ähnlich ablaufen.
Es sei 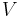 eine Verschiebung längs des Pfeiles
eine Verschiebung längs des Pfeiles 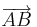 und
und 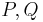 zwei beliebige Punkte der Ebene mit ihren Bildern
zwei beliebige Punkte der Ebene mit ihren Bildern 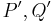 bei
bei 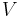 , die voneinander verschieden sind und nicht auf dem Pfeil
, die voneinander verschieden sind und nicht auf dem Pfeil 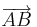 liegen.
liegen.
Wir haben zu zeigen, dass 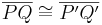 ist. Es genügt natürlich zu zeigen, dass
ist. Es genügt natürlich zu zeigen, dass 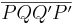 ein Parallelogramm ist, da in jedem Parllelogramm die gegenüberliegenden Seiten gleich lang sind.
ein Parallelogramm ist, da in jedem Parllelogramm die gegenüberliegenden Seiten gleich lang sind.
--Steph85
| Beweisschritt | Begründung |
|---|---|
1) 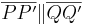
|
folgt unmittelbar aus der Definition der Verschiebung |
2) 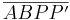 ist ein Parallelogramm. ist ein Parallelogramm.
|
folgt unmittelbar aus der Definition der Verschiebung ("Das Bild des Punktes  ist der fehlende Eckpunkt des Parallelogramms ist der fehlende Eckpunkt des Parallelogramms 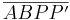 .") .")
|
3) 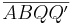 ist ein Parallelogramm. ist ein Parallelogramm.
|
folgt unmittelbar aus der Definition der Verschiebung |
4) Aus 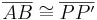 und und 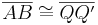 folgt folgt 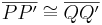
|
(2), (3), Transitivität |
5) 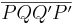 ist ein Parallelogramm. ist ein Parallelogramm.
|
(1), (4) |

