Übung Aufgaben 9 (SoSe 11): Unterschied zwischen den Versionen
| Zeile 8: | Zeile 8: | ||
[[Lösung von Aufg. 9.2 (SoSe_11)]] | [[Lösung von Aufg. 9.2 (SoSe_11)]] | ||
| − | |||
== Aufgabe 9.3 == | == Aufgabe 9.3 == | ||
Aktuelle Version vom 31. Mai 2011, 13:32 Uhr
Inhaltsverzeichnis |
Aufgabe 9.1
Beweisen Sie: Zu jeder Strecke 
existiert genau eine Strecke 
mit 
und 
.
Lösung von Aufg. 9.1 (SoSe_11)
Aufgabe 9.2
Beweisen Sie: Zu jeder Strecke existiert genau eine Strecke mit 
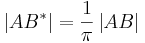und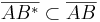 
.
Lösung von Aufg. 9.2 (SoSe_11)
Aufgabe 9.3
Definieren Sie noch einmal die Begriffe Halbgerade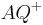 
und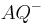 
. In diesen neuen Definitionen dürfen Sie die Zwischenrelation nicht explizit verwenden. Beweisen Sie dann, dass Ihre neuen Definitionen zur | Definition II.5 äquivalent sind.
Lösung von Aufg. 9.3 (SoSe_11)
Aufgabe 9.4
Beweisen Sie: Jede Strecke hat höchstens einen Mittelpunkt.
Lösung von Aufgabe 9.4 (SoSe_11)
Aufgabe 9.5
Beweisen Sie: Der Durchschnitt zweier konvexer Punktmengen ist konvex.
Lösung von Aufg. 9.5 (SoSe_11)
Aufgabe 9.6
Formulieren Sie die Kontraposition der Implikation aus Aufgabe 9.5.
Lösung von Aufg. 9.6 (SoSe_11)
Aufgabe 9.7
Zeigen Sie mittels einer Skizze, dass die Umkehrung der Implikation aus Aufgabe 9.5 nicht wahr ist.
