Lösung von Aufg. 12.6 WS 11/12: Unterschied zwischen den Versionen
Aus Geometrie-Wiki
(Die Seite wurde neu angelegt: „Beweisen Sie:<br /> <u>Korollar 1 zum schwachen Außenwinkelsatz</u><br /> ::In jedem Dreieck sind mindestens zwei Innenwinkel spitze Winkel. [[Category:Einfü…“) |
|||
| (6 dazwischenliegende Versionen von 3 Benutzern werden nicht angezeigt) | |||
| Zeile 2: | Zeile 2: | ||
<u>Korollar 1 zum schwachen Außenwinkelsatz</u><br /> | <u>Korollar 1 zum schwachen Außenwinkelsatz</u><br /> | ||
::In jedem Dreieck sind mindestens zwei Innenwinkel spitze Winkel. | ::In jedem Dreieck sind mindestens zwei Innenwinkel spitze Winkel. | ||
| + | |||
| + | Beweis: | ||
| + | Vor.: <math>\overline{ABC}</math> mit <math>\ \beta , \alpha & \gamma </math> | ||
| + | Beh.: <math>\ | \alpha | < 90 </math>, <math>\ | \beta | < 90 </math> | ||
| + | Ann.: <math>\ | \alpha | = 90 </math>, <math>\ | \beta | = 90 </math> Was wäre es denn, wenn <math>\alpha</math> oder <math>\beta</math> größer 90 sind? Dies müsste auch noch untersucht werden. --[[Benutzer:Andreas|Tutor Andreas]] 14:26, 16. Jan. 2012 (CET) | ||
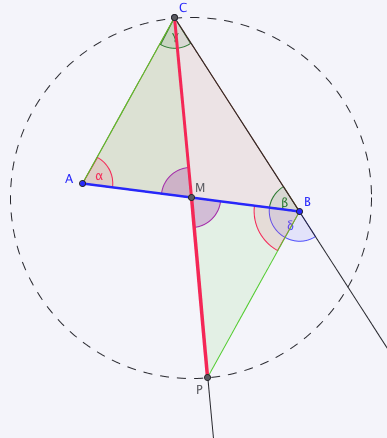
| + | [[Datei:Bildschirmfoto 2012-01-15 um 13.31.23.png]] | ||
| + | |||
| + | 1) M sei Mittelpunkt von Strecke AB / Existenz und Eindeutigkeit des Mittelpunkts | ||
| + | 2) Es existiert P Element MC- mit Abstand MC=MP / Axiom vom Lineal | ||
| + | 3) lila Winkel = lila Winkel / Scheitelwinkelsatz | ||
| + | 4) Strecke AM kongruent zu MB / (1), Def. Mittelpunkt | ||
| + | 5) Strecke CM kongruent zu MP / (2) | ||
| + | 6) Dreieck AMC kongruent zu Dreieck BMP / (3), (4), (5), SWS | ||
| + | 7) <math>\ | \alpha | =\angle PBM = 90 </math> / (6), Vor. | ||
| + | 8) <math>\ | \beta | = | \delta | =90 </math> / Supplementaxiom, Vor. | ||
| + | 9) <math>\ | \delta | =\angle PBM = 90 </math> / (7), (8) | ||
| + | 10) BC- kongruent zu BP'+ / (9),Winkelkonstruktionsaxiom | ||
| + | 11) P ist Element von BC / (10) | ||
| + | |||
| + | 12) Analog lässt sich zeigen, dass P Element von AB | ||
| + | |||
| + | 13) AC kongruent zu BC / (11), (12), Axiom I.1 | ||
| + | 14) koll(ABC) / 13), Def. koll -> Widerspruch zur Vorrausetzung | ||
| + | |||
| + | --[[Benutzer:Flobold|Flobold]] 13:56, 15. Jan. 2012 (CET)<br /> | ||
| + | @Flobold, kannst du bitte mal mit Worten erklären, warum du den schwachen Außenwinkelsatz nochmal vollständig beweist?<br /> | ||
| + | Mir ist auch nicht --[[Benutzer:RicRic|RicRic]] 08:01, 16. Jan. 2012 (CET)klar, wo du die Annahme verwendest.<br /><br /> | ||
| + | |||
| + | Vor.: Dreiek ABC<br /> | ||
| + | Beh.: Dreick ABC hat mindestens zweii spitze innenwinkel<br /> | ||
| + | Ann.: o.B.d.A. <math>\left| \beta \right| < 90 \wedge \left| \alpha \right| < 90</math><br /> | ||
| + | Beweis: | ||
| + | |||
| + | {| class="wikitable sortable" | ||
| + | !Schritt!!Begründung | ||
| + | |- | ||
| + | | (1) <math>\left| \beta \right| > 90</math> || Annahme | ||
| + | |- | ||
| + | | (2) <math>\exists \beta' : ist Nebenwikel von \beta </math> || | ||
| + | |- | ||
| + | | (3) <math>\left| \beta' \right| < 90</math> || (2),(1) Nebenweikel sind sublimäntär | ||
| + | |- | ||
| + | | (4) <math>\left| \alpha \right| < \left| \beta' \right| \lightning</math> zur Vorr q.e.d.|| Schwacher Ausenwinkelsatz, <math>\left| \beta' \right|</math> ist Außenwikel, <math>\left| \alpha \right|</math> ist nicht anliegender Innenwinkel. (3) | ||
| + | |}--[[Benutzer:RicRic|RicRic]] 21:06, 16. Jan. 2012 (CET)Muss heißen größer gleich und nicht nur größer --[[Benutzer:RicRic|RicRic]] 20:20, 17. Jan. 2012 (CET) | ||
[[Category:Einführung_Geometrie]] | [[Category:Einführung_Geometrie]] | ||
Aktuelle Version vom 19. Januar 2012, 10:52 Uhr
Beweisen Sie:
Korollar 1 zum schwachen Außenwinkelsatz
- In jedem Dreieck sind mindestens zwei Innenwinkel spitze Winkel.
Beweis: Vor.:mit Fehler beim Parsen(Syntaxfehler): \ \beta , \alpha & \gamma
Beh.:,
Ann.:
,
Was wäre es denn, wenn
oder
größer 90 sind? Dies müsste auch noch untersucht werden. --Tutor Andreas 14:26, 16. Jan. 2012 (CET)
1) M sei Mittelpunkt von Strecke AB / Existenz und Eindeutigkeit des Mittelpunkts 2) Es existiert P Element MC- mit Abstand MC=MP / Axiom vom Lineal 3) lila Winkel = lila Winkel / Scheitelwinkelsatz 4) Strecke AM kongruent zu MB / (1), Def. Mittelpunkt 5) Strecke CM kongruent zu MP / (2) 6) Dreieck AMC kongruent zu Dreieck BMP / (3), (4), (5), SWS 7)/ (6), Vor. 8)
/ Supplementaxiom, Vor. 9)
/ (7), (8) 10) BC- kongruent zu BP'+ / (9),Winkelkonstruktionsaxiom 11) P ist Element von BC / (10)
12) Analog lässt sich zeigen, dass P Element von AB
13) AC kongruent zu BC / (11), (12), Axiom I.1 14) koll(ABC) / 13), Def. koll -> Widerspruch zur Vorrausetzung
--Flobold 13:56, 15. Jan. 2012 (CET)
@Flobold, kannst du bitte mal mit Worten erklären, warum du den schwachen Außenwinkelsatz nochmal vollständig beweist?
Mir ist auch nicht --RicRic 08:01, 16. Jan. 2012 (CET)klar, wo du die Annahme verwendest.
Vor.: Dreiek ABC
Beh.: Dreick ABC hat mindestens zweii spitze innenwinkel
Ann.: o.B.d.A. 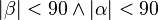
Beweis:
| Schritt | Begründung |
|---|---|
(1) 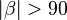 |
Annahme |
(2) 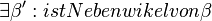 |
|
(3) 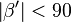 |
(2),(1) Nebenweikel sind sublimäntär |
| (4) Fehler beim Parsen(Unbekannte Funktion „\lightning“): \left| \alpha \right| < \left| \beta' \right| \lightning zur Vorr q.e.d. | Schwacher Ausenwinkelsatz, 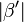 ist Außenwikel, ist Außenwikel, 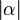 ist nicht anliegender Innenwinkel. (3) ist nicht anliegender Innenwinkel. (3)
|