Das Lot von einem Punkt auf eine Gerade: Unterschied zwischen den Versionen
Aus Geometrie-Wiki
TimoRR (Diskussion | Beiträge) (→Beweis der Existenz und Eindeutigkeit des Lotes:) |
(→Definition IX.2: (Abstand eines Punktes zu einer Geraden)) |
||
| (Eine dazwischenliegende Version von einem Benutzer wird nicht angezeigt) | |||
| Zeile 7: | Zeile 7: | ||
===== Definition IX.2: (Abstand eines Punktes zu einer Geraden) ===== | ===== Definition IX.2: (Abstand eines Punktes zu einer Geraden) ===== | ||
:: Es sei <math>\ P</math> ein Punkt außerhalb von <math>\ g</math>. Der Abstand von <math>\ P</math> zu <math>\ g</math> ist ... | :: Es sei <math>\ P</math> ein Punkt außerhalb von <math>\ g</math>. Der Abstand von <math>\ P</math> zu <math>\ g</math> ist ... | ||
| − | :: ... die Länge | + | :: ... die Länge des Lotes <math> \overline {PL} </math> von <math>\ P</math> auf <math>\ g</math>. --[[Benutzer:Löwenzahn|Löwenzahn]] 16:06, 9. Jul. 2010 (UTC) |
== Existenz und Eindeutigkeit des Lotes == | == Existenz und Eindeutigkeit des Lotes == | ||
| Zeile 53: | Zeile 53: | ||
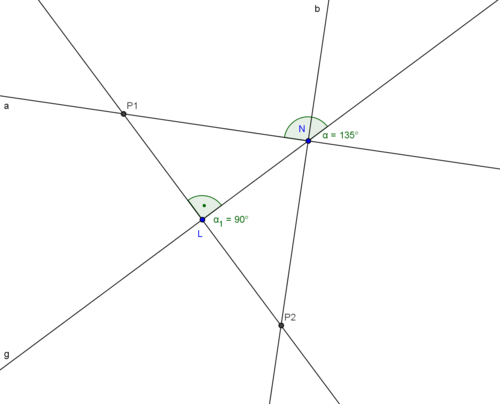
[[Bild:Lot2.png|500px]] | [[Bild:Lot2.png|500px]] | ||
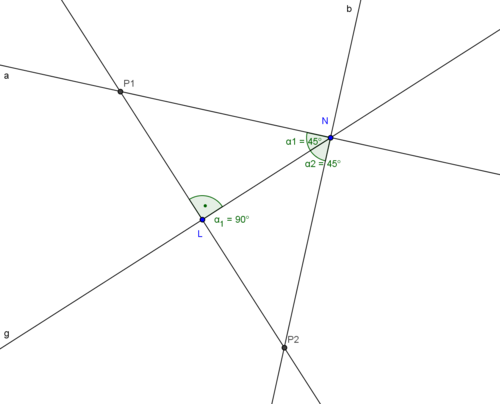
| − | <math> \overline{P1L} </math>ist Lot von P auf g <br /> | + | <math> \overline{P1L} </math>ist Lot von P auf g. <br /> |
| − | Annahme:<math> \exists N \in g mit \overline{P1N} ist auch Lot von P auf g, | + | Annahme: <math> \exists N \in g </math> mit <math>\overline{P1N} </math> ist auch Lot von P auf g, <math> L \not\equiv N.</math> <br /> <math>\alpha1 </math> ist bezüglich <math> \alpha </math> nicht anliegender Innenwinkel (<math>\overline{NLP1}</math>) --> Widerspruch, weil <math> \alpha1 < \alpha </math> (schwacher Außenwinkelsatz) |
| − | + | ||
| − | + | ||
Aktuelle Version vom 26. Juli 2010, 11:05 Uhr
Inhaltsverzeichnis |
Der Begriff des Lotes
Definition IX.1: (Lot, Lotgerade, Lotfußpunkt)
- Es sei
 ein Punkt, der nicht zur Geraden
ein Punkt, der nicht zur Geraden  gehören möge. ...
gehören möge. ...
- ...Die Gerade
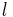 , die senkrecht auf
, die senkrecht auf  steht und durch den Punkt
steht und durch den Punkt  geht heißt Lotgerade von
geht heißt Lotgerade von  auf
auf  . Der Schnittpunkt
. Der Schnittpunkt  von
von 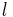 mit
mit  , heißt Lotfußpunkt des Lotes von
, heißt Lotfußpunkt des Lotes von  auf
auf  . Unter dem Lot von
. Unter dem Lot von  auf
auf  , versteht man die Strecke
, versteht man die Strecke 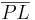 . --Löwenzahn 16:01, 9. Jul. 2010 (UTC)
. --Löwenzahn 16:01, 9. Jul. 2010 (UTC)
- Es sei
Definition IX.2: (Abstand eines Punktes zu einer Geraden)
- Es sei
 ein Punkt außerhalb von
ein Punkt außerhalb von  . Der Abstand von
. Der Abstand von  zu
zu  ist ...
ist ...
- ... die Länge des Lotes
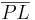 von
von  auf
auf  . --Löwenzahn 16:06, 9. Jul. 2010 (UTC)
. --Löwenzahn 16:06, 9. Jul. 2010 (UTC)
- Es sei
Existenz und Eindeutigkeit des Lotes
Satz IX.1: (Existenz und Eindeutigkeit des Lotes)
- Zu jedem Punkt
 außerhalb einer Geraden
außerhalb einer Geraden  gibt es genau ein Lot von
gibt es genau ein Lot von  auf
auf  .
.
- Zu jedem Punkt
Beweis der Existenz und Eindeutigkeit des Lotes:
| Beweisschritt | Begründung | |
|---|---|---|
| (I) | Konstruiere einen Punkt N auf g. Fall 1: Falls 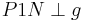 , dann ist , dann ist 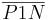 unser Lot. unser Lot.Fall 2: 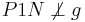 , dann weiter mit (II) , dann weiter mit (II)
|
Konstruktion, (Gerade ist Menge von Punkten) |
| (II) | Antragen von 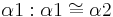
|
Konstruktion, Winkelkonstruktionsaxiom |
| (III) | Antragen von 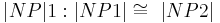
|
Konstruktion, Axiom vom Lineal |
| (IV) | Antragen von 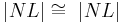
|
trivial |
| (V) | 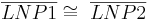
|
(II), (III), (IV), SWS |
| (VI) | 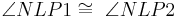
|
beides rechte Winkel --> 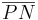 ist Lot auf g. ist Lot auf g.
|
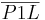 ist Lot von P auf g.
ist Lot von P auf g.
Annahme: 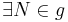 mit
mit 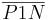 ist auch Lot von P auf g,
ist auch Lot von P auf g, 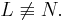
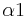 ist bezüglich
ist bezüglich  nicht anliegender Innenwinkel (
nicht anliegender Innenwinkel (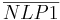 ) --> Widerspruch, weil
) --> Widerspruch, weil 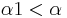 (schwacher Außenwinkelsatz)
(schwacher Außenwinkelsatz)