Benutzer:*m.g.*: Unterschied zwischen den Versionen

Aus Geometrie-Wiki
Wechseln zu: Navigation, Suche
 
(127 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt)
Zeile 1: Zeile 1:
−
[[Benutzer:*m.g.*/Test Quiz|Quiz-Text]]
+
[[alt]]
 +
[[Schreibtest]]
 +
[[Die WIKI-Seiten für die Sekundarstufe_SoSe_17]]<br />
 +
[[TÜ_27_04_18]]<br />
 +
[[TÜ_04_05_18]]<br />
 +
[[TÜ Algebra 01]]
 +
[[TÜ021118]]
  
−
{{#ev:youtube|F6PMPJcC68Y}}
+
[[ Übung 00 ]]<br />
  
−
<flash>file=HDV.swf|width=350px|height=200px|quality=best</flash>
+
[[dreielementige Gruppe]]
 +
[[Schreibumgebung]]<br />
 +
[[Elementare Funktionen]]<br />
 +
 
 +
[[Didaktik der Bruchrechnung]]<br />
 +
 
 +
[[Allgemeiner Teil]]<br />
 +
 
 +
[[Indoorcycling gegen Prüfungsangst]]
 +
[[2013]]
 +
[[Quiz_Definition_1]]
 +
 
 +
[[Quiz_Definition_2]]
 +
 
 +
[[Quiz_Definition_3]]
 +
 
 +
[[Ellipse]]
 +
[[Schreibtest_mg]]
 +
[[Sommersemester_2012]]<br />
 +
[[Test]] <br />
 +
[[Zwischenspeicher]]
 +
[[TKS]]
 +
[[Vorlage Aufgabe]]
 +
=Aufgaben zum Abstand=
 +
 
 +
==Aufgabe 5.1==
 +
<u>'''Satz:'''</u>
 +
::Es seien <math>A,B</math> und <math>C</math> drei paarweise verschiedene Punkte.<br />
 +
::Wenn der Punkt <math>B</math> zwischen den Punkten <math>A</math> und <math>C</math> liegt, dann liegt weder <math>A</math> zwischen <math>B</math> und <math>C</math> noch <math>C</math> zwischen <math>A</math> und <math>B</math>.
 +
Beweisen Sie diesen Satz.
 +
 
 +
<br />
 +
[[Lösung von Aufgabe 5.1_S (WS_12_13)]]
 +
 
 +
==Aufgabe 5.2==
 +
Es seien <math>A</math>, <math>B</math>, <math>C</math> und <math>D</math> vier paarweise verschiedene Punkte. <br />
 +
Beweisen Sie:<br />
 +
<math>\overline{CD} \subset \overline{AB} \Rightarrow \forall P \in \overline{CD}: \operatorname{Zw}(APB}</math>.
 +
 
 +
 
 +
 
 +
<br /><br />
 +
[[Lösung von Aufgabe 5.2_S (WS_12_13)]]
 +
 
 +
==Aufgabe 5.3==
 +
Zeigen Sie, dass für drei paarweise verschiedene Punkte <math>\ A, B</math> und <math>\ C</math> gilt:<br />
 +
Wenn <math> C \in \ AB^{+} </math> und <math>\left| AB \right| < \left| AC \right| </math> dann gilt <math>\operatorname Zw (A, B, C) </math>
 +
 
 +
<br />
 +
[[Lösung von Aufgabe 5.3_S (WS_12_13)]]
 +
 
 +
 
 +
==Aufgabe 5.4==
 +
Beweisen Sie: Zu jeder Strecke <math>\overline{AB} </math> existiert genau eine Strecke <math>\overline{AC} </math> auf <math>\ AB^{+} </math> mit <math>\left| AB \right| = \frac{1}{4} \left| AC \right| </math> und <math>\overline{AB} </math> <math> \subset</math>  <math>\overline{AC} </math>
 +
<br />
 +
 
 +
<br /><br />
 +
[[Lösung von Aufgabe 5.4_S (WS_12_13)]]
 +
 
 +
=Weitere Aufgabe zur Inzidenz=
 +
 
 +
 
 +
== Aufgabe 5.5 ==
 +
Beweisen Sie: Je vier nicht komplanare Punkte sind paarweise verschieden (Hinweis: Nutzen Sie bei der Beweisführung die Sätze aus Aufgabe 4.3 und Zusatzaufgabe 4.4).<br /><br />
 +
[[Lösung von Aufg. 5.5_S (WS_12_13)]]<br />
 +
<br />

Aktuelle Version vom 27. April 2020, 11:41 Uhr

alt Schreibtest Die WIKI-Seiten für die Sekundarstufe_SoSe_17
TÜ_27_04_18
TÜ_04_05_18
TÜ Algebra 01 TÜ021118

Übung 00

dreielementige Gruppe Schreibumgebung
Elementare Funktionen

Didaktik der Bruchrechnung

Allgemeiner Teil

Indoorcycling gegen Prüfungsangst 2013 Quiz_Definition_1

Quiz_Definition_2

Quiz_Definition_3

Ellipse Schreibtest_mg Sommersemester_2012
Test
Zwischenspeicher TKS Vorlage Aufgabe

Inhaltsverzeichnis

Aufgaben zum Abstand

Aufgabe 5.1

Satz:

Es seien 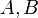A,B und C drei paarweise verschiedene Punkte.
Wenn der Punkt B zwischen den Punkten A und C liegt, dann liegt weder A zwischen B und C noch C zwischen A und B.

Beweisen Sie diesen Satz.


Lösung von Aufgabe 5.1_S (WS_12_13)

Aufgabe 5.2

Es seien A, B, C und D vier paarweise verschiedene Punkte.
Beweisen Sie:
Fehler beim Parsen(Syntaxfehler): \overline{CD} \subset \overline{AB} \Rightarrow \forall P \in \overline{CD}: \operatorname{Zw}(APB} .




Lösung von Aufgabe 5.2_S (WS_12_13)

Aufgabe 5.3

Zeigen Sie, dass für drei paarweise verschiedene Punkte \ A, B und \ C gilt:
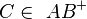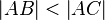Wenn C \in \ AB^{+} und \left| AB \right| < \left| AC \right| dann gilt \operatorname Zw (A, B, C)


Lösung von Aufgabe 5.3_S (WS_12_13)


Aufgabe 5.4

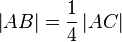Beweisen Sie: Zu jeder Strecke \overline{AB} existiert genau eine Strecke \overline{AC} auf \ AB^{+} mit \left| AB \right| = \frac{1}{4} \left| AC \right| und \overline{AB} \subset \overline{AC}



Lösung von Aufgabe 5.4_S (WS_12_13)

Weitere Aufgabe zur Inzidenz

Aufgabe 5.5

Beweisen Sie: Je vier nicht komplanare Punkte sind paarweise verschieden (Hinweis: Nutzen Sie bei der Beweisführung die Sätze aus Aufgabe 4.3 und Zusatzaufgabe 4.4).

Lösung von Aufg. 5.5_S (WS_12_13)

Von „http://geometrie.zum.de/index.php?title=Benutzer:*m.g.*&oldid=34815“