Serie 4 SoSe 2013: Unterschied zwischen den Versionen
*m.g.* (Diskussion | Beiträge) (→Aufgabe 4.05) |
*m.g.* (Diskussion | Beiträge) (→Aufgabe 4.06) |
||
| Zeile 34: | Zeile 34: | ||
==Aufgabe 4.06== | ==Aufgabe 4.06== | ||
Sie dürfen davon ausgehen, dass für jedes Dreieck gilt: Der größeren zweier Seiten liegt der größere Innenwinkel gegenüber.<br /> | Sie dürfen davon ausgehen, dass für jedes Dreieck gilt: Der größeren zweier Seiten liegt der größere Innenwinkel gegenüber.<br /> | ||
| − | Formulieren Sie die Umkehrung dieser Seiten-Winkel-Beziehung und beweisen Sie | + | (o.B.d.A.: <math>a>b \Rightarrow |\alpha| > |\beta|</math>) |
| + | Formulieren Sie die Umkehrung dieser Seiten-Winkel-Beziehung und beweisen Sie diese Umkehrung mittels eines Widerspruchsbeweises.<br /> | ||
| + | (Der Basiswinkelsatz sei auch schon bewiesen.) | ||
[[Lösung von Aufgabe 4.06_S SoSe 13]] | [[Lösung von Aufgabe 4.06_S SoSe 13]] | ||
Version vom 11. Mai 2013, 17:35 Uhr
Aufgabe 4.01Der Innenwinkelsatz für Dreiecke sei bereits bewiesen. Aufgabe 4.02Es sei n eine beliebige natürliche Zahl, die größer als 2 ist. Entwickeln Sie eine Abbildungsvorschrift, die jedem solchen n die Innenwinkelsumme des entsprechenden n-Ecks zuordnet. Aufgabe 4.03a) Wie lautet der Stufenwinkelsatz? (schauen Sie bei Bedarf in Schulbüchern nach). Lösung von Aufgabe 4.03_S SoSe 13
Aufgabe 4.04Es seien Aufgabe 4.05Wir gehen davon aus, dass wir der ebenen Geometrie ein kartesisches Koordinatensystem zugrunde gelegt haben. Bezüglich dieses Systems definieren wir die folgenden beiden Punktmengen: Beweisen Sie Aufgabe 4.06Sie dürfen davon ausgehen, dass für jedes Dreieck gilt: Der größeren zweier Seiten liegt der größere Innenwinkel gegenüber.
|
 und
und  . Welche der folgenden Aussagen repräsentiert den Stufenwinkelsatz bzw. ist eine zu diesem Satz äuivalente Aussage (Begründen Sie jeweils)?
. Welche der folgenden Aussagen repräsentiert den Stufenwinkelsatz bzw. ist eine zu diesem Satz äuivalente Aussage (Begründen Sie jeweils)?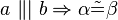
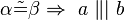
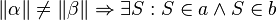
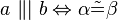
 und
und  zwei Punktmengen. Was müssen Sie konkret zeigen, wenn Sie beweisen wollen, dass
zwei Punktmengen. Was müssen Sie konkret zeigen, wenn Sie beweisen wollen, dass 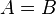 ?
?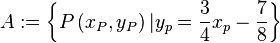
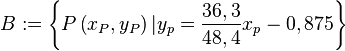
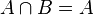 .
.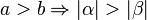 )
Formulieren Sie die Umkehrung dieser Seiten-Winkel-Beziehung und beweisen Sie diese Umkehrung mittels eines Widerspruchsbeweises.
)
Formulieren Sie die Umkehrung dieser Seiten-Winkel-Beziehung und beweisen Sie diese Umkehrung mittels eines Widerspruchsbeweises.
