Geradenspiegelungen als Bewegungen mit genau einer Fixpunktgeraden (2010): Unterschied zwischen den Versionen

Aus Geometrie-Wiki
Wechseln zu: Navigation, Suche
(→‎Beweis von Lemma 4.1)
 
Zeile 52: Zeile 52:
 
# <math>\ Zw(A,B,P)</math>
 
# <math>\ Zw(A,B,P)</math>
 
Die Abstandserhaltung von <math>\ \phi</math> sowie die Sätze [[Bewegungen_(2010)#Satz_1.3:_.28Zwischenrelation_als_Invariante_von_Bewegungen.29|1.3]] und [[Bewegungen_(2010)#Satz_1.4:_.28Geradentreue.2C_Halgeradentreue.2C_Streckentreue.2C_Schnittpunkttreue_bei_Bewegungen.29|1.4]] helfen den Beweis zu führen.
 
Die Abstandserhaltung von <math>\ \phi</math> sowie die Sätze [[Bewegungen_(2010)#Satz_1.3:_.28Zwischenrelation_als_Invariante_von_Bewegungen.29|1.3]] und [[Bewegungen_(2010)#Satz_1.4:_.28Geradentreue.2C_Halgeradentreue.2C_Streckentreue.2C_Schnittpunkttreue_bei_Bewegungen.29|1.4]] helfen den Beweis zu führen.
 +
 +
 +
{| class="wikitable center"
 +
|+ Beweis<br />
 +
 +
|- style="background: #DDFFDD;"
 +
! Nr.
 +
! Beschreibung des Schrittes
 +
! Begründung der Korrektheit des Schrittes
 +
|-
 +
| 1.
 +
| Es sei P Element der Geraden <math>\overline {AB}</math>
 +
| Konstruktion
 +
|-
 +
| 2.
 +
| Es gilt entweder
 +
|# <math>\ Zw(A,P,B)</math> oder
 +
|# <math>\ Zw(P,A,B)</math> oder
 +
|# <math>\ Zw(A,B,P)</math>
 +
| Umkehrung der Dreiecksgleichung
 +
|-
 +
| 3.
 +
| Also gilt <math>\|AP| + |PB| = |AB|</math> oder ANALOG
 +
| (2), Definition "zwischen"
 +
|-
 +
| 4.
 +
| <math>\|AP| = |A'P'|, |PB| = |P'B'|, |AB| = |A'B'|</math>
 +
| (3), Definition Bewegung
 +
|-
 +
| 5.
 +
| Also gilt: P = P'
 +
| (4), Axiom vom Lineal
 +
|-
 +
|
 +
|}
 +
P wird also auf sich selbst abgebildet; und wenn (beispielhaft) bei der Bewegung jeder Punkt der Geraden wieder auf sich selbst abgebildet wird, so ist die Gerade eine Fixpunktgerade bzgl. dieser Bewegung. --[[Benutzer:Nicola|Nicola]] 18:20, 25. Dez. 2010 (UTC)
  
 
===Beweis von Satz 4.2===
 
===Beweis von Satz 4.2===

Aktuelle Version vom 25. Dezember 2010, 19:20 Uhr

Inhaltsverzeichnis

Satz 4.1

Jede Geradenspiegelung besitzt genau eine Fixpunktgerade.

Beweis von Satz 4.1

Beweis von Shaun15

Die folgende Beweisführung wurde von User Shaun15 am 02.11. in morgentlicher Frühe geführt. Vielen Dank dafür. (Aus Gründen der Übersicht habe ich ein wenig umformatiert (nur ein paar Zeilenumbrüche) . --*m.g.* 14:21, 2. Nov. 2010 (UTC))

1.Existenz

Es sei g eine Gerade und A, B, C drei voneinander verschiedene Punkte.
Weiter möge gelten A, B nicht Є g und C Є g. Zz: Bei Spiegelung an g wird P auf P` abgebildet.
Nach Def. Spiegelung wird C auf C` abgebildet und A auf A`.
Da P Є g wird P` ebenfalls auf g abgebildet. Sodass gilt: |AP|=|A`P`|, |CP|=|C`P`| und |AC|=|A`C`|.
Bleibt zz: P = P`.
Dies folgt unmittelbar aus der Abstandstreue von Bewegungen.
Angenommen P` würde nicht mit P zusammenfallen, so gäbe es drei Möglichkeiten.
1. |AP|=|A`P`| aber |CP|≠|C`P`| oder
2. |CP|=|C`P`| aber |AP|≠|A`P`| oder
3. |AP|≠|A`P`| aber |CP|≠|C`P`|.
Jede dieser Möglichkeiten währe ein Wiederspruch zur Abstandstreue.
Daraus folgt. P = P`
Daraus folgt. g ist Fixpunktgerade (demnach gibt es Fixpunktgeraden bei einer Spiegelung)

Ich glaube der Beweis wird ab dem Zeitpunkt hinfällig, wenn man annimmt, dass 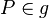P \in g gilt. Dadurch gilt nach Definition 2.1: (Spiegelung an der Geraden \ g), dass \ P = \ P' . --Andreas 15:03, 2. Nov. 2010 (UTC)

2.Bei einer Spiegelung gibt es höchstens eine Fixpunktgerade

Es seien zwei Geraden g und h mit A, B Є g und C, D Є h.
Im Folgenden betrachten wir die Spiegelung an g.
Es gibt drei Fälle:
1. g identisch h: g = h also ein und dieselbe und somit eine Fixpunktgerade.
2. g parallel zu h: nach Def. ist g Mittelsenkrechte von |CC`| und |DD`|. |CD| verschieden von |C`D`|. also ist h keine Fixpunktgerade. Bleibt nur g. Also auch hier nur eine Fixpunktgerade.
3. g ∩ h ={P}: P ist Fixpunkt auf g und auf h. (Bew.1.Existenz) Nach Def. ist g Mittelsenkrechte von |CC`| und |DD`|. Somit ist kein weiterer Punkt von h Fixpunkt. Also bleibt g wieder einzige Fixpunktgerade.

Satz 4.2

Wenn eine Bewegung \ \phi genau eine Fixpunktgerade \ g hat, so ist sie eine Geradenspiegelung.

--*m.g.* 13:30, 4. Nov. 2010 (UTC): Der Beweis wird einfacher, wenn man ein Teiproblem auslagert und im Rahmen eines Hilfssatzes bearbeitet:

Lemma 4.1

Wenn ein Bewegung \ \phidie beiden Fixpunkte \ A und \ B besitzt, dann ist die Gerade \ AB eine Fixpunktgerade bezüglich \ \phi.


Frage: Wenn wir die Fixpunktgeradendefinition von Tja??? verwenden ("Eine Fixgerade f einer Abbildung φ, bei der (mindestens) zwei Punkt der Fixgeraden f bei der Abbildung φ auf sich selbst abgebildet werden, heißt Fixpunktgerade."), können wir uns das Lemma sparen, oder? -Steph85

Beweis von Lemma 4.1

Es sei \ \phi eine Bewegung mit den beiden Fixpunkten \ A und \ B. Ferner sei \ P ein weiterer von \ A und \ B jeweils verschiedener Punkt der Geraden \ AB.

zu zeigen: Der Punkt \ P wird durch \ \phi auf sich selbst abgebildet.

Es können genau drei Fälle auftreten:

  1. \ Zw(A,P,B)
  2. \ Zw(P,A,B)
  3. \ Zw(A,B,P)

Die Abstandserhaltung von \ \phi sowie die Sätze 1.3 und 1.4 helfen den Beweis zu führen.


Beweis
Nr. Beschreibung des Schrittes Begründung der Korrektheit des Schrittes
1. Es sei P Element der Geraden \overline {AB} Konstruktion
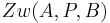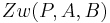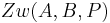
2. Es gilt entweder # \ Zw(A,P,B) oder # \ Zw(P,A,B) oder # \ Zw(A,B,P) Umkehrung der Dreiecksgleichung
3. Also gilt 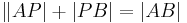\|AP| + |PB| = |AB| oder ANALOG (2), Definition "zwischen"
4. 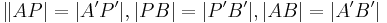\|AP| = |A'P'|, |PB| = |P'B'|, |AB| = |A'B'| (3), Definition Bewegung
5. Also gilt: P = P' (4), Axiom vom Lineal

P wird also auf sich selbst abgebildet; und wenn (beispielhaft) bei der Bewegung jeder Punkt der Geraden wieder auf sich selbst abgebildet wird, so ist die Gerade eine Fixpunktgerade bzgl. dieser Bewegung. --Nicola 18:20, 25. Dez. 2010 (UTC)

Beweis von Satz 4.2

Es sei \ \phi eine Bewegung.

Voraussetzung

\ \phi hat genau eine Fixpunktgerade. Es sei dieses die Gerade \ g.

Behauptung

\ \phi ist eine Geradenspiegelung.

Beweisführung

Wir werden zeigen, dass \ \phi die Spiegelung an der Geraden \ g ist.

Entsprechend Definition 2.1 haben wir folgendes zu zeigen:

  1. Jeder Punkt von \ g wird durch \ \phi auf sich selbst abgebildet: 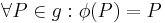\forall P \in g: \phi (P) =P
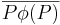  2. Für alle Punkte, die nicht zu \ g gehören, gilt: Die Gerade \ g ist die Mittelsenkrechte der Strecke \overline{P \phi (P)}.

Der Beweis von 1. ergibt sich unmittelbar aus der Voraussetzung, dass \ g bezüglich \ \phi eine Fixpunktgerade ist.

Es bleibt zu zeigen:
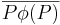Für jeden Punkt \ P außerhalb der Geraden \ g gilt: (*) \ g ist die Mittelsenkrechte der Strecke \overline{P \phi (P)}.

Es sei \ P ein beliebiger Punkt, der nicht auf der Geraden \ g liegt.

Um (*) zu beweisen werden wir wie folgt vorgehen:

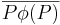  1. Wir zeigen, dass die Gerade \ g und die Strecke \overline{P \phi (P)} einen gemeinsamen Schnittpunkt \ M haben.
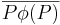  2. Wir zeigen, dass dieser Schnittpunkt \ M der Mittelpunkt der Strecke \overline{P \phi (P)} ist.
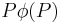  3. Wir zeigen, dass die Gerade \ g senkrecht auf der Geraden \ P \phi (P) steht.
Von „http://geometrie.zum.de/index.php?title=Geradenspiegelungen_als_Bewegungen_mit_genau_einer_Fixpunktgeraden_(2010)&oldid=5865“