Lösung von Aufgabe 5.1 (WS 11/12): Unterschied zwischen den Versionen

Aus Geometrie-Wiki
Wechseln zu: Navigation, Suche
Zeile 20: Zeile 20:
 
<br /> * Aber das Beispiel von RicRic macht es deutlich. Die Eigenschaft der Relation muss für alle Elemente gelten und im Beispiel von RicRic gilt eben nicht, dass Ungleichheit in <math>\mathbb{R}</math> transitiv ist. Es reicht nicht einen Fall zu finden für den es gilt. --[[Benutzer:Todah raba|Todah raba]] 17:08, 13. Nov. 2011 (CET)Genau!--[[Benutzer:Tutorin Anne|Tutorin Anne]] 19:44, 16. Nov. 2011 (CET)
 
<br /> * Aber das Beispiel von RicRic macht es deutlich. Die Eigenschaft der Relation muss für alle Elemente gelten und im Beispiel von RicRic gilt eben nicht, dass Ungleichheit in <math>\mathbb{R}</math> transitiv ist. Es reicht nicht einen Fall zu finden für den es gilt. --[[Benutzer:Todah raba|Todah raba]] 17:08, 13. Nov. 2011 (CET)Genau!--[[Benutzer:Tutorin Anne|Tutorin Anne]] 19:44, 16. Nov. 2011 (CET)
 
<br />aber das Beispiel von RicRic ist doch nicht ganz richtig? es gilt ja: a <math>\neq </math> b und b <math>\neq </math> c dann ist auch a <math>\neq </math> c.  Demenstprechend kann man ja nicht sagen 1 ist ungleich 2 und 3 ist ungleich 2 , sondern 2 ist dann ungleich 3 und dann stimmt auch wieder, dass 3 ungleich 1 ist. Ich denke , dass (6) auch tranisitiv ist. --[[Benutzer:Cmhock|Cmhock]] 14:52, 18. Nov. 2011 (CET)
 
<br />aber das Beispiel von RicRic ist doch nicht ganz richtig? es gilt ja: a <math>\neq </math> b und b <math>\neq </math> c dann ist auch a <math>\neq </math> c.  Demenstprechend kann man ja nicht sagen 1 ist ungleich 2 und 3 ist ungleich 2 , sondern 2 ist dann ungleich 3 und dann stimmt auch wieder, dass 3 ungleich 1 ist. Ich denke , dass (6) auch tranisitiv ist. --[[Benutzer:Cmhock|Cmhock]] 14:52, 18. Nov. 2011 (CET)
 +
* Aber a, b und c müssen nicht zwangsläufig unterschiedlich sein. Man muss ja alle Zahlen aus <math>\mathbb{R}</math> unabhängig von einander für a,b und c einsetzen können, also kann es ja auch <math>3\neq 5\wedge 5\neq 3\Rightarrow 3\neq 3</math> heißen und damit ist Transitivität bei der Ungleichheitsrelation ausgeschlossen.--[[Benutzer:BeaBer|BeaBer]] 21:11, 18. Nov. 2011 (CET)

Version vom 18. November 2011, 21:11 Uhr

Entscheiden Sie für die folgenden Relationen, ob es sich um reflexive, symmetrische sowie transitive Relationen handelt?

  • Parallelität von Geraden der Ebene
  • Kongruenz geometrischer Figuren
  • Teilbarkeit in \mathbb{N}
  • Kleinerrelation in \mathbb{R}
  • Größer-Gleich-Relation in \mathbb{R}
  • Ungleichheit in \mathbb{R}

(1) reflexiv, symmetrisch, transitiv
(2) reflexiv, symmetrisch, transitiv
(3) reflexiv, trannsitiv

  • Nur zur Ergänzung der Begrifflichkeiten und für die, die es interessiert: Diese Relation ist ist zwar nicht symmetrisch, aber antisymmetrisch.--Tutor Andreas 10:48, 10. Nov. 2011 (CET)

(4) transitiv
(5) reflexiv, transitiv
(6) symmetrisch, transitiv
--Pinky* 21:48, 8. Nov. 2011 (CET)
Ich denke (6) ist nur symmetrisch, nicht transitiv,Bps.: 1 nicht gleich 2 und 3 nicht gleich 2 aber 2 gleich 2--RicRic 14:07, 10. Nov. 2011 (CET)
Meiner Meinung ist (6) auch transitiv, da z.B. Wurzel 2 ungleich Wurzel 4 und Wurzel 4 ungleich Wurzel 9 dann ist auch Wurzel 2 ungleich Wurzel 9
* Aber das Beispiel von RicRic macht es deutlich. Die Eigenschaft der Relation muss für alle Elemente gelten und im Beispiel von RicRic gilt eben nicht, dass Ungleichheit in \mathbb{R} transitiv ist. Es reicht nicht einen Fall zu finden für den es gilt. --Todah raba 17:08, 13. Nov. 2011 (CET)Genau!--Tutorin Anne 19:44, 16. Nov. 2011 (CET)
aber das Beispiel von RicRic ist doch nicht ganz richtig? es gilt ja: a \neq b und b \neq c dann ist auch a \neq c. Demenstprechend kann man ja nicht sagen 1 ist ungleich 2 und 3 ist ungleich 2 , sondern 2 ist dann ungleich 3 und dann stimmt auch wieder, dass 3 ungleich 1 ist. Ich denke , dass (6) auch tranisitiv ist. --Cmhock 14:52, 18. Nov. 2011 (CET)

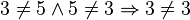  • Aber a, b und c müssen nicht zwangsläufig unterschiedlich sein. Man muss ja alle Zahlen aus \mathbb{R} unabhängig von einander für a,b und c einsetzen können, also kann es ja auch 3\neq 5\wedge 5\neq 3\Rightarrow 3\neq 3 heißen und damit ist Transitivität bei der Ungleichheitsrelation ausgeschlossen.--BeaBer 21:11, 18. Nov. 2011 (CET)
Von „http://geometrie.zum.de/index.php?title=Lösung_von_Aufgabe_5.1_(WS_11/12)&oldid=9469“