Aufgabe 12.01
Mark definiert: Es sei  ein rechtwinkliges Dreieck. Die längste Seite von ein rechtwinkliges Dreieck. Die längste Seite von  heißt Hypotenuse von heißt Hypotenuse von  . .
Diskutieren Sie Marks Definition.
Lösung von Aufgabe 12.01_SoSe_13
Aufgabe 12.02
Definieren Sie die Begriffe Kreistangente, Berührungspunkt einer Kreistangente und Berührungsradius einer Kreistangente.
Lösung von Aufg. 12.02_SoSe_13
Aufgabe 12.03
Alles in ein und derselben Ebene:
Es sei  ein Kreis mit dem Mittelpunkt ein Kreis mit dem Mittelpunkt  . Ferner seien . Ferner seien  ein Punkt von ein Punkt von  und und  eine Gerade durch eine Gerade durch  , die senkrecht auf , die senkrecht auf  steht. Beweisen Sie: steht. Beweisen Sie:  ist Tangente an ist Tangente an  im Punkt im Punkt  . .
Lösung von Aufg. 12.03_SoSe_13
Aufgabe 12.04
Die Gerade  sei Tangente an den Kreis sei Tangente an den Kreis  (Mittelpunkt (Mittelpunkt  ) im Punkt ) im Punkt  . Beweisen Sie: . Beweisen Sie: 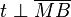 . .
Lösung von Aufg. 12.04_SoSe_13
Aufgabe 12.05
Lösung von Aufg. 12.05_SoSe_13
Aufgabe 12.06
Lösung von Aufg. 12.06_SoSe_13
Aufgabe 12.07
Lösung von Aufg. 12.07_SoSe_13
Aufgabe 12.08
Lösung von Aufgabe 12.08_SoSe_13
Aufgabe 12.09
Lösung von Aufgabe 12.09_SoSe_13
Aufgabe 12.10
|  ein rechtwinkliges Dreieck. Die längste Seite von
ein rechtwinkliges Dreieck. Die längste Seite von  ein Kreis mit dem Mittelpunkt
ein Kreis mit dem Mittelpunkt  . Ferner seien
. Ferner seien  ein Punkt von
ein Punkt von  eine Gerade durch
eine Gerade durch  steht. Beweisen Sie:
steht. Beweisen Sie: 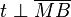 .
.

