Übung Aufgaben 7 (SoSe 11)
Inhaltsverzeichnis |
Aufgabe 7.1
Frau Schultze-Kröttendörfer beginnt die letzte Geometriestunde in ihrer 4. Klasse mit der folgenden Frage: „In der letzten Woche haben wir ganz viele Geraden gezeichnet. Wer weiß denn noch was eine Gerade ist?“
Warum ist diese Frage nicht nur aus didaktischer Sicht sinnlos?
Lösung von Aufg. 7.1 (SoSe_11)
Aufgabe 7.2
Oberstudienrat Kramer beginnt die Stunde zur analytischen Geometrie mit der Frage, ob denn jemand wüsste, wie eine Gerade im 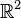 definiert wäre. Vergleichen Sie mit Aufgabe 1.
definiert wäre. Vergleichen Sie mit Aufgabe 1.
Lösung von Aufg. 7.2 (SoSe_11)
Aufgabe 7.3
Die Eigenschaft der Komplanarität ist das räumliche Analogon zur Kollinearität in der Ebene. Formulieren Sie eine Definition der Relation „komplanar“.
Lösung von Aufg. 7.3 (SoSe_11)
Aufgabe 7.4
Satz I: Je drei nicht kollineare Punkte sind paarweise verschieden.
- Wir formulieren Satz I neu und beginnen mit „Es seien
 ,
,  und
und  drei Punkte.“ Ergänzen Sie: „Wenn
drei Punkte.“ Ergänzen Sie: „Wenn  ,
, und
und  … , dann … .“
… , dann … .“
- Beweisen Sie Satz I indirekt.
- Bilden Sie die Kontraposition von Satz I.
- Beweisen Sie auch die Kontraposition von Satz I.
- Formulieren Sie die Umkehrung von Satz I.
- Gilt auch die Umkehrung von Satz I?
Lösung von Aufg. 7.4 (SoSe_11)
Aufgabe 7.5
Axiom I/1 sagte aus, dass es zu je zwei verschiedenen Punkten genau eine Gerade gibt, zu der die beiden Punkte gehören. Für die räumliche Geometrie gibt es ein analoges Axiom. Wir wollen es mit Axiom I/4 bezeichnen. Formulieren Sie dieses Axiom I/4.
Lösung von Aufg. 7.5 (SoSe_11)
Aufgabe 7.6
Satz II: Je vier nicht komplanare Punkte sind paarweise verschieden.
Formulieren Sie Teilaufgaben, die zu den Teilaufgaben a) bis f) von Aufgabe 4 analog sind und lösen Sie dann diese Teilaufgaben.
Lösung von Aufg. 7.6 (SoSe_11)
Aufgabe 7.7 (*)
Es seien 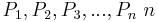 verschiedene Punkte der Ebene, von denen je drei stets nicht kollinear sind. Wie viele verschiedene Geraden gibt es, die jeweils durch zwei dieser
verschiedene Punkte der Ebene, von denen je drei stets nicht kollinear sind. Wie viele verschiedene Geraden gibt es, die jeweils durch zwei dieser  Punkte gehen?
Hinweis: Es gibt eine Problemlösestrategie: Führe einen komplizierten Fall auf einen einfacheren Fall zurück. Carl Friedrich Gauß hilft auch bei der Lösung dieser Aufgabe.
Punkte gehen?
Hinweis: Es gibt eine Problemlösestrategie: Führe einen komplizierten Fall auf einen einfacheren Fall zurück. Carl Friedrich Gauß hilft auch bei der Lösung dieser Aufgabe.
Im Praktikum haben wir eine analoge Aufgabe einmal mit Schülern einer 7. Hauptschulklasse gelöst. Formulieren Sie obige Aufgabe für Schüler dieser Schulstufe.

