Geradenspiegelungen
Inhaltsverzeichnis |
Konstruktion des Bildes eines Punktes  bei einer Spiegelung an der Geraden
bei einer Spiegelung an der Geraden 
Übungsaufgabe
Es sei  ein Punkt der Ebene der nicht zur Geraden
ein Punkt der Ebene der nicht zur Geraden  dieser Ebene gehört.
Erstellen Sie eine Konstruktionsbeschreibung für die Konstruktion des Bildes von
dieser Ebene gehört.
Erstellen Sie eine Konstruktionsbeschreibung für die Konstruktion des Bildes von  bei der Spiegelung an
bei der Spiegelung an  . Begründen Sie jeweils die Korrektheit eines jeden Ihrer Konstruktionsschritte.
. Begründen Sie jeweils die Korrektheit eines jeden Ihrer Konstruktionsschritte.
| Nr. | Beschreibung des Schrittes | Genauere Beschreibung | Begründung der Korrektheit des Schrittes |
|---|---|---|---|
| 1. | Wir fällen das Lot von  auf auf  . Den Schnittpunkt des Lotes mit der Geraden . Den Schnittpunkt des Lotes mit der Geraden  bezeichnen wir mit bezeichnen wir mit 
|
Existenz und Eindeutigkeit des Lotes So bestimmen wir die kürzeste Strecke zwischen dem Punkt  und der Geraden und der Geraden  . Außerdem steht das Lot senkrecht auf . Außerdem steht das Lot senkrecht auf  , was die Voraussetzung dafür ist, dass , was die Voraussetzung dafür ist, dass  später Mittelsenkrechte werden kann. später Mittelsenkrechte werden kann.
|
Existenz und Eindeutigkeit des Lotes + Existenz und Eindeutigkeit des Schnittpunktes 
|
| 2. | Nun tragen wir die Strecke 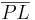 auf der Halbgeraden auf der Halbgeraden 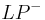 ab ab
|
Axiom vom Lineal (Eindeutigkeit des Streckenabtragens auf einem Strahl) Durch das Abtragen der Strecke bekommen wir auf beiden Seiten der Halbgeraden den gleichen Abstand vond er Geraden 
|
Existenz und Eindeutigkeit des Streckenabtragens |
| 3. | Den entstandenen Punkt bezeichnen wir mit 
|
 ist der Bildpunkt von P bei der Geradenspiegelung an ist der Bildpunkt von P bei der Geradenspiegelung an  . Das wird dadurch ersichtlich, dass . Das wird dadurch ersichtlich, dass  und und  den gleichen Abstand zu den gleichen Abstand zu  haben und haben und  somit Mittelsenkrechte der Strecke somit Mittelsenkrechte der Strecke 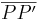 ist. ist.
|
Axiom vom Lineal -geändert Tunichtgut- |
Bemerkung --*m.g.* 16:20, 1. Nov. 2010 (UTC):
Mit der Korrektheit ist hier etwas anderes gemeint ... .
Definition des Begriffs
Definition 2.1: (Spiegelung an der Geraden  )
)
- Es sei
 eine Gerade. Unter der Geradenspiegelung
eine Gerade. Unter der Geradenspiegelung 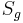 versteht man eine ....
versteht man eine ....
- Es sei
- Es sei
 eine Gerade und P ein Punkkt der Ebene. Unter der Geradenspiegelung
eine Gerade und P ein Punkkt der Ebene. Unter der Geradenspiegelung 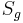 versteht man eine Abbildung der Ebene auf sich:
versteht man eine Abbildung der Ebene auf sich:
- Es sei
(1) Für den Fall dass P 
 : P = P'
: P = P'
(2) Für den fall dass P 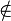
 : Die Gerade
: Die Gerade  ist Mittelsenkrechte der Strecke zwischen dem Punkt P und seinem Bildpunkt P'
ist Mittelsenkrechte der Strecke zwischen dem Punkt P und seinem Bildpunkt P'
Alternativ?
Es seien eine Gerade g und zwei Punkte A, A'  g. s ist genau dann Spiegelgerade des Punktes A, wenn gilt: s ist Mittelsenkrechte der Strecke AA'[Balken drüber].
g. s ist genau dann Spiegelgerade des Punktes A, wenn gilt: s ist Mittelsenkrechte der Strecke AA'[Balken drüber].
Bemerkungen --*m.g.* 15:49, 1. Nov. 2010 (UTC):
"Balken drüber": \overline{AA'}:
Handelt es sich wirklich um eine Definition des Begriffs Geradenspiegelung
oder doch eher um eine Definition des Begriffs Spiegelgerade?
Beide hängen natürlich eng miteinander zusammen, aber wenn Geradenspiegelung zu definieren ist ... .
Macht es Sinn einem Punkt seine Spiegelgerade zuzuordnen ("s ist genau dann Spiegelgerade des Punktes A")
Die Geradenspiegelung als spezielle Bewegung
Satz 2.1: (Abstandserhaltung von Geradenspiegelungen)
- Jede Geradenspiegelung
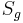 ist eine abstandserhaltende Abbildung.
ist eine abstandserhaltende Abbildung.
- Jede Geradenspiegelung
Beweis von Satz 2.1:
Es seien  ,
,  zwei Punkte, die an einer Geraden
zwei Punkte, die an einer Geraden  auf ihre Bilder
auf ihre Bilder 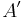 und
und 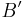 gespiegelt werden.
gespiegelt werden.
Wir unterscheiden drei Fälle:
Fall 1
Der Beweis ist trivial, da es sich bei dieser speziellen Geradenspiegelung um die Identität handelt.
Bemerkung --*m.g.* 16:01, 1. Nov. 2010 (UTC):
Auch wenn wir Umlaufsinn bisher nirgends definiert haben,
wissen wir, dass jede Geradenspieglung den Umlaufsinn verändert.
Kann eine Geradenspeigelung damit die Identität sein?
Sie meinen nicht, dass die jweils betrachtete Geradenspiegelung die Identität ist,
sondern, dass jeder Punkt der Spiegelgeradenauf sich selbst abgebildet wird.
Fall 2


 ,
, 
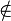

Den Schnittpunkt von 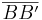 mit
mit  bezeichnen wir mit
bezeichnen wir mit 
| Nr. | Beschreibung des Schrittes | Begründung der Korrektheit des Schrittes |
|---|---|---|
| 1. |  = = 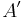
|
Definition Geradenspiegelung |
| 2. | 
|
 ist Mittelsenkrechte von ist Mittelsenkrechte von 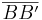
|
| 3. | 
|
Es handelt sich um dieselbe Gerade. |
| 4. | 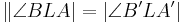 = 90° = 90°
|
 ist Mittelsenkrechte von ist Mittelsenkrechte von 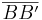
|
| 5. | 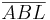 kongruent kongruent 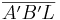
|
2. + 3. + 4. + SWS |
| 6. | 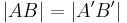
|
5. |
Fall 3
Den Schnittpunkt von 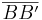 mit
mit  bezeichnen wir mit
bezeichnen wir mit 
Den Schnittpunkt von 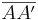 mit
mit  bezeichnen wir mit
bezeichnen wir mit 
| Nr. | Beschreibung des Schrittes | Begründung der Korrektheit des Schrittes |
|---|---|---|
| 1. | 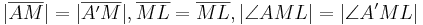 = 90° = 90°
|
 ist Mittelsenkrechte von ist Mittelsenkrechte von 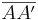
|
| 2. | 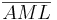 kongruent kongruent 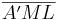
|
1. |
| 3. |  und und 
|
Wechselwinkelsatz, da 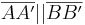
|
| 4. | 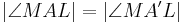 --> --> 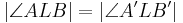
|
2. + 3. |
| 5. | 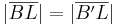
|
 ist Mittelsenkrechte von ist Mittelsenkrechte von 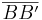
|
| 6. | 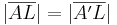
|
2. |
| 7. | 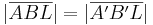
|
4. + 5. + 6. + SWS |
| 8. | 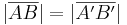
|
7. |
Ergänzung: Für den Fall, das A und B nicht in der selben Halbebene bezüglich der Geraden s liegt, läuft der Beweis analog, nur dass die Winkel anderst benannt werden müssen.
Müsste es bei Fall 3 Schritt 5 nicht  ist Mittelsenkrechte von
ist Mittelsenkrechte von 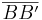 heißen oder bezieht man hier Fall 2 mit ein, sodass der Beweis formal und logisch richtig ist? Ja
heißen oder bezieht man hier Fall 2 mit ein, sodass der Beweis formal und logisch richtig ist? Ja 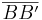 ist korrekt, habs geändert.
ist korrekt, habs geändert.
Vielen Dank :) --Andreas 16:02, 30. Okt. 2010 (UTC)
Bemerkung--*m.g.* 16:44, 1. Nov. 2010 (UTC):
soweit ich sehe ist der Beweis korrekt.
Fall 2 dürfte, da er bereits bewiesen wurde, verwendet werden.
Vielleicht doch zwei Unterfälle:und
in derselben Halbebene bezüglich
und
und
in verschiedenen Halbebenen bezüglich
?
Eindeutige Bestimmtheit von Geradenspiegelungen
Bestimmung über die Spiegelgerade
Satz 2.2
- Zu jeder Geraden gibt es genau eine Geradenspiegelung.
Anders ausgedrückt: Eine Geradenspieglung ist durch die Angabe ihrer Spiegelachse eindeutig bestimmt.
Möglicher Beweis von Satz 2.2
1.(es gibt mindestens eine)
Es sei eine Gerade g und ein Punkt P nicht Є g. Ich konstruiere P´ dermaßen, dass gilt: g ist Mittelsenkrechte von |PP´|. Nach Def. ist dies eine Geradenspiegelung an g.
- Damit ist die Existenz bewiesen.
2. (es gibt höchstens eine)
Um zu zeigen dass es nicht mehr Geradenspiegelungen geben kann, nehme ich an, dass es mindestens zwei Geradenspiegelungen an einer Geraden gibt.
So konstruiere ich also P´´ so, dass g die Mittelsenkrechte von |P´P´´| ist (dies möge auf dem Bild so sein).
Bleibt also z.z.: P = P´´
Kann ich das zeigen bin ich fertig, denn dann habe ich wieder die Identität und das "Spiegelspielchen" könnte von neuem beginnen. Also nehme ich an: P ≠P``
Es möge gelten: |PP´| ∩ g = Q und |P`P``| ∩ g = R
Ich betrachte das Dreieck ∆P´QR:
Es gilt also nach Konstruktion (Ich geh einfach mal davon aus ich könnte so etwas konstruieren) bzw. Def. Spiegelung an einer Geraden: |<P´QR = <P`RQ = 90°|(Wiederspruch zum Satz über die Innenwinkelsumme im Dreieck)
Also ist P = P´´.
- Damit ist bewiesen, dass es nicht mehr als eine Spiegelung geben kann. --Shaun15 23:23, 2. Nov. 2010 (UTC)
Satz 2.3
- Eine Geradenspiegelung
 ist durch die Angabe eines Punktes
ist durch die Angabe eines Punktes  und dem Bild von
und dem Bild von 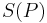 eindeutig bestimmt, falls
eindeutig bestimmt, falls 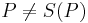 gilt.
gilt.
- Eine Geradenspiegelung
Dieser Satz gilt, da nach Definition Geradenspiegelung die Spiegelgerade s die Mittelsenkrechte der Strecke 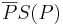 ist und diese Mittelsenkrechte exisitert und eindeutig ist. --Tja??? 16:40, 2. Nov. 2010 (UTC)
ist und diese Mittelsenkrechte exisitert und eindeutig ist. --Tja??? 16:40, 2. Nov. 2010 (UTC)