|
|
| (74 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt) |
| Zeile 1: |
Zeile 1: |
| − | = Halbebenen und das Axiom von Pasch =
| + | [[alt]] |
| − | == Halbebenen ==
| + | [[Schreibtest]] |
| − | === Analogiebetrachtungen ===
| + | [[Die WIKI-Seiten für die Sekundarstufe_SoSe_17]]<br /> |
| | + | [[TÜ_27_04_18]]<br /> |
| | + | [[TÜ_04_05_18]]<br /> |
| | + | [[TÜ Algebra 01]] |
| | + | [[TÜ021118]] |
| | | | |
| − | {| class="wikitable center"
| + | [[ Übung 00 ]]<br /> |
| − | | style="background: #DDFFDD;"| <center>'''Halbgeraden'''</center>
| + | |
| − | | style="background: #DDFFDD;"| <center>'''Halbebenen'''</center>
| + | |
| | | | |
| − | |-
| + | [[dreielementige Gruppe]] |
| − | | <ggb_applet width="398" height="401" version="3.2" ggbBase64="UEsDBBQACAAIAGSMwjwAAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1s1Vlbb9s2FH5efwUhFMWGIbIoWbKF2imyrg8BsiVdsmIYhgG0RMtcdHElypcW/e87vMiW7FhR3KQXP0TmRYeH3+VQckavVkmMFjQvWJaODWxaBqJpkIUsjcZGyacnQ+PV6bNRRLOITnKCplmeED42HNM2RH/JTp/9MCpm2RKRWE55x+hybExJXFADFfOckrCYUcob/aRcsZiRfH05+Y8GvNgOqCDn6byEVXheQl+QhBesqJo9ueA8ZvxXtmAhzVGcBWPDcyF1+PaO5pwFJB4bfUv12GPD3hmELkeMzrKcfchSLqZvg0+hB6GCfaBwpyX6Rj250REtg5iFjKRiMzIPmITQkoV8BiH9IYSkLJoJgHxfRQuyLA+v1wWnCVr9TfNsbJxg7Auk16o5dEWjgLxgQdeSI/WWDEMX15RzoKVAZEW3gEU5CxuN8+KXLN52zTOW8tdkzstccurormu+FgvAWrlI+CyNYqr7MEA+o8HtJFtdSxCwo0LfrOfyFpnQJHqdxVmOcgGvCxP0daKuco7IdDPLknMsOUPHEEE349i35Qx5nairnBWzVKWmd46rXWOrWoYVSHQIGEGKm83HZEKBWgOVKeMXVQMkcLvdqrjh9zKZgAfqItjExI8Vc9Tbkc/oluYpjZVIUuC2zMoCLYQY1VoykZAGLIGmGtCQEEHXn5CA6g1plNMqceUgBZgctepC3Oke9aokRA4F5BpwKAWwHy72IpzKwSVjIzEj00Ah4aJXWCGmCQWfcKkJKakNNmfGpihk0t+Vk/X4FmUY3lORiyX94kLi+YxAppUJYrIGv9c3JSP+loXNrZIUIJP7ANvNRQBBypzSUNc4rpWM5hBS+qKGuASqQCvIAaocWoNhHRODtz+ou+UkZSJhf7mwqxlWqNyDz9uj8Kn7R2L1tdEZmK5t1T+uAss27f7DwAqyJCFpiFKSwMIX4HeJEBOnACKWUBQiWACnUCl5NRCpUDrAHu6idGxgjYxmNeEzMG1Ki0JktNl073husOuoymXZndm5nE4LygWcnqe1ZreRt4X/xDL9vrzFNp0mEY6CH4jwXG/bjXfraQsC9H2q5hSqqrEEjtyA8Xbq/iDrrsxN2pnLIVKF+eQwcX5n4hoSTkOmDADTL/Vsil5E/CXaEPZEtempCNxFoo1ASUQsrH2ecjikqCz6+2fPLaVzcehfpjc5SQvx8Kfm1M60A0q4khWvqYVoTwRX7SJols2ro8omthV18vqtlM6h6dveEFvW0MMD3xkq52PT83z4OB72nL6NRUU4vowe9OLVHg1Bdy8GX8qL8SEvCvNtrfhZdNa8iE0XC4t5ztDx3AH8kZw45qBO1MDXlPjmwHJs13d8x3Xh9aL//Tjzmkaif0cbV4fqdNiujUJHq6gNv4g+SPvjkdUqCa+bJCzTHdyhCFBK32pIQhXrk4HZdwbeVhLO9yOJdxAzy7ue3GW7IhYqWMVleVgQdpsgmq9btX0eR3rHOnDXSbwWEX31SLsN3WVDtVcuTWxAck4LeAXUO+bQlkcloqu5wPxonvar+uJBPC0ehaf7X10ehaa7yvJanJT7RfwrkAa9OYQWRUvDsjTU1BL10MLYIaB3HzXL74kay/Rs28We7TsYDzB8q8qmPfD7ntvHbt/xh7735gQ/AT3tPFDNw+rH5U93AZ+WCc1ZYGzniyVho2W13f3ddYYU35/fDV1xrHN88b7M+Muzt/9+/PkTUg1jP2MOdxjN25/wPeiR1MKKC3JD/2oeT/qH1wIImFY5qx9hQSaaanvPgapo+0Ndpl3Xb3zqD9D3Q2/vQX/yEOjtzi8oD3/q/VaRd70K+YNQN0CbZFlMwaoVJmTXYTV9dhLxcSC5d/4E46tTpN8C4f0ichoiev5PtqC5qGwfr95+et5dTE53H38+BE+tE8e0Bg1f6kNBPFc1HrfsQyrq1X+elv+R0f+SOv0fUEsHCKhmSd+1BQAAxBoAAFBLAQIUABQACAAIAGSMwjyoZknftQUAAMQaAAAMAAAAAAAAAAAAAAAAAAAAAABnZW9nZWJyYS54bWxQSwUGAAAAAAEAAQA6AAAA7wUAAAAA" framePossible = "false" showResetIcon = "true" showAnimationButton = "true" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "true" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" allowRescaling = "true" />
| + | [[Schreibumgebung]]<br /> |
| | + | [[Elementare Funktionen]]<br /> |
| | | | |
| − | | <ggb_applet width="396" height="402" version="3.2" ggbBase64="UEsDBBQACAAIAC+LwjwAAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1s3V3rbttGFv69fQpCKIp2GzNzv6B2iyipXTduE8PZYrHdbkFJtMxYFlWKSuwUfaN9in2yPTND6kpRoi4xlSAAw+FwNPN955w558xwcvzd/V3PexcmwyjunzSwjxpe2G/HnajfPWmM0usj1fju28+Ou2HcDVtJ4F3HyV2QnjSoTxqmfBR9+9nfjoc38Xsv6Nkqv0Th+5PGddAbhg1vOEjCoDO8CcN0pjwY3Ue9KEgeXrXehu10OHngGjnvD0bwK2kygrL2XeciGua3T+0PDnpR+iJ6F3XCxOvF7ZOG4NB1+NcvYZJG7aB30mDIlZCTBpl7CEXUPL2Jk+hD3E9N9Unj11DiecPoQwhvIlN2/NQO9DgctXtRJwr6ZjC2H1DJ895HnfQGmtQCmgyj7k3qft221o7jpHP1MEzDO+/+X2ES2+74EiGJCVcaSSp4w3twjzDV8EjAaBTFlFMNGEKHoSdM+5ohgSWXEmuJmXlp+TP72+G7qzBNgcuhF9yHE5S7SdSZuTkfNuPepGgQR/30eTBIR4kVBJoVXaUP5ucAucSM8lm/2wuzMgI83YTt21Z8f2WRw9Q1/eZhYF+xHWp1n8e9OPESAwIMoJtdW+5q65iejmshWwfZGlkbptHxc6yJrWGvLXe1tXpR33UtGznOR41R/jPR0DMF0LiR3/Hge0ErBHloeKN+lF7kNyA3t9lQsXvh59FdCxRnWnLGbeJdtXn8dE7mjm/DpB/2nGT1gdtRPBp674wEu9+yHemE7egObt2DDJLA0PUP6IAr7YTdJMw77tTOAWafzkjvXPHx07wTpg9D6Gs7BfsB40nNWIx6p6BaJ407v+s3vE6QmlKjP73wLgTlSq1MWJEaY/OsMbYksTUKufpnzycow+NC+bCSFPQGNwGU+NkAesEDmIjpIdn2foo7swMN+gCYHQVo6sA0YCgZhGEnM4tpJsfeAJq0WjGFt4Vp6N2fNI6wz0ANhdCMYcww0wz01JUrKSiVQlNCCGXQ/gfXtm3CKZixJ7ZbNGPfIbYCu+angR3yFZrgpgjmDjqwlkJIKQXjgmtNlK4GXTu+uwv6Ha8f3EE3LsAyWLwiM8l4ATKy5wXYwOgwGqX5g65rKmtggQVjZMYgdxuzdie9AfXuh0PQZj6B4OkmTHFsqTKXily9ur4ehqkBV2oHpi5jckqOAXSCFBeYUCEIRZzY94lPFJEYI66IoDDXWCqITylBhDAMj7hQnM1b4RI0wj/6rs7Q2cLoDmb3dpRW0YDLT0UDxKykZxpAfSy0AI9AY4KQNlxspwDNaAggxcm6itCqoAit5YpAyhRhdq5czRjanK8pOS8Q6Icl4v/BmnEuucbAEVYCc8pkiaTPD3ddSZ/l67yfgk8AEM2R1XVktRbIel5O1qzmPF/UnHWIEMwyYS4td9kBF9jXGKScEMUUk4wi6sgQPuOaMkop14ghTS0X3JcU7sDyCM4IEpRvog0voh74J8V6gM1gvIBkkM6A/OyLYBAPv/kdVwF78tKjmqtpyLEvmdRgdQBABDbcIc4AW8yUoBCiICIq+iprIHy5GuHLTRC+XI5wVfuyI4i1DxYdIMYaMwouoAOYgCHhmAnCGYMoUG7l0hQi3FyNcHMThJt1k2EQYSQzcK1/nTkqTEokmcZIEcTYVlNmuZFYw0qQTawEqQvCYCWYz4TWglGisEL5LEmljyVCGCuNBBgQyfdnKNawFJVQvqwbylr7UjEIGAXThIDsZpYCcZ8KDTYEwWOpMNufqVjDVlTCuFk3jDGmEGSOA0yQWAsyZeB5cIEQxO4CohixDcSvkvQm7sb9oFcQal4uc9raFTzs9iF52EsCySLH2zjY0pcYiDCGnGKETRJg3w52KWGZlW8vENapQFjnkAgrjoiWBEQwLzCMsWaUY3AWhXhctprL2AorsBV+smxBhEWUJooq8JeQZvoj8LUsfG07qjoLVL2oMsO8qFH4ykxuQAiYPmBi4Vpyls/gPsza8JdKCGKBDr7D+HUFvOECvN9Xgff7+sCrfI441kjB/C0ZyHWWVxe+UAyBU8rgD+VM7RDcn6IkWUiSdZfZmMB5OxUsTf7GAdmbhcwYW5IYztxU6iOttWKUco4Y5/ufzpdpRMfxNsXSDHunVfTitD56AYQIzbhSHEvQD5OCz4Iz6mPElJIEIgrgbJdZs2UYh+UYn1XB+Kw+GGPiUyWIEJwwopHUeWymfA1xmUYamxQPZWyHGL+Oew/g5xT7o6cuTjuDCy1K2P8SQbPtW5zx8Tt29a9d/a69ZxCHrM79uE7kmI/b3YXJmloDmWYQczq93jVttnAVBpcvHg3Drrmb2OHfdzOgYoksGc/GEsmMI8eIUIQppoR0mXLswwQINlZReMaVduKofMo4kRLEkUkkd7ViYeWtZ1azxtYgivuLmxFuw3BgdoG86r9Jgv7QbCFydaY2OazJ0/WBsbQ4WapHmSwfgaruwanU0YJO8XzrxpxW0WzRmxGozLhJ7Suk1eGS1aonWZPdC9lCICXrUVkx51Rp+8KjU7n+0gRZY2WCVnHJJi/VJJ97RMzWCMwJ1loKgpXMdBbmPDq1DYuqnSfNT1djfLrJ+trpVutr+/B+CfE5VlhQs8UUE0UzbeRU+1SC3mAO8YUget/L8merIT/bBPKz+kGumI8pByNl1obHIR3jwpeAqsncmbgD7xvx5mrEm5sYkmbdDAnIONNEaI2FFBwwdnZE+EgBD5wTjSkG0B91FZltYqtZXSB+zFXk0zVQPt1khfN0qxXO/eQqkE844MgYk9p+QmBdHyEBUGxT0EbQd5kmLTPWpZCfbQL5Wf0gZ8TE2MZ1FBBCTBL/hEtfwwOEGVz2P0FWWcivZEyadTMmH2Mhf0vXegNjXRd0D8Kt3sBM18ZiHKBLvYGJrg/cB+dOb2Cc62I8PoYrvWRtJAPCrZCMb8hEIN1qyZLVqXxtY7qVYBwauvWT6Xa64xuzkrIeb8WrKVstA8+wPPNZSb8TuY9SoPqrrPb//vsivIbf6Px69VulVB2tIg8Vll5mYu8tR//xksUKrIRSnAowHVrahT+T15c+WBEMgm+XY5WbHsGaEx8CHooxIpQilENZy/TiihWY3YnqhKxiSb3y/u5deV/00m+8MVF7XwMwIaqZkQmTlDABJssSy7hvJgMC1HIiNSNuwYZRDm4oAT+JgxQogQ+X2O4+iN07XfNqmH9dMa+H2YoN0synwnxdB7O7ofhw+WptxddjrbHNqRdGPPfECvXriAlfMMSYguiZQrjBdrVf8SOszBRuHptxUbrLQseNA8h6eYJrh5FbfZxTiPNpOc6nm+J8ujXOe9kDRpT0tbF2oCFSYLfcyRhMTpTDJEa0yYns9LvJQtTPylE/2xT1s5qiLnzKkTTfnWGGpHROIISZPuPm22Blgh+2yxi+EPVmOerNTVFv1tGmLESXRcGl3MqglAaXBSFmQaBZEG6uFXQWhJ7TrV8vtt6dK5qEotsHpKtcDLS7sLQsKC07/oLwKoJUOSzdCwK7OdqjilvMl7jFMtv/UiVAnR9yzfzi64Mmbt4/Jqws/DxiRCCfwzyPNQIvipZuGKw5cd1DJm5e4VRxOohm+lYlDq05ba1Dpm3tcLQwGuX6cGib9exeb+TN5Uf2ZRyYS+WNnEdYZZtqSw+i2uVxbBBpYk0VFiY4Eiw/UQkJzcG+gmJSIbMtvRs6jFeZTsw6jK+dG3e54PIF5T7Zgiuyi4PFVjpg5+Xe+44+BceTbT4QBOnshDcC5YRpiYgxnVQz55cIn4MthQiWaGpOWyrbYF3lULGPkPtZcWZTsCATV1UCs6u11XdtrjfX7RK+fw5+tvza6wd3LVIvvmC77gcJ0Gr6nQ3pTXifQp/gwUnjiz9GcfpN9/I/f379l/u3fX8WsRReaMy+vR1o5Qtn6+sKL8MuGl4Eb8J/zopZdiTtMEyi67zT7nha0cjlO9sYP0yDJH1t0HVQXXhfe18efQlO4ldPPOTLrzZIL1wuSyxcVk8pXC5LJjzS4Uzm40klpVQwQ0jBtRD5h1QYa6k5o+DSSUlIxfmhWIDJggAfVRDg9fe7VQ+x1xdfVivxLZO1H1ZJ2RJPs3anQh7ZynaeRLs7NPZ89RlpBwcQ3iVAP34q8OwFnZefGjqVlWudpPEPbu48z/cP/eiSti8X5tIs8Upc/RtXO3K137q07u2qibYwlUt2vKuoyGmcPsM95xMX8EmX87l+wuFmjwPaecSTCxeaF656LmCXIx8dEvJoTq2PyCFD//aQoD/6pKT+9pBO58ml/igXe1Zv6Gfn0OdQmMRRZz6R5ma2X3944sFE+sT78Yn38rdxl/JaF1Xi0IsNvZdK2whKprsizrDK1YVs5qC14rgXBhMP4NwOEt4chQss7dFKTCc4JolfnJ2Zg4kohSUYWJ/Oln3+7/hdmBjJ/fNZ86/P1wuy6UyQPdXE68u/Pl8/2t7+y9R6pIGyLMf0WdOSIZbZZyaZMPuGNKfmeCM0c7bsNNZPp/+nF3Of/5dQ3/4fUEsHCM8TtlY4DQAARGoAAFBLAQIUABQACAAIAC+LwjzPE7ZWOA0AAERqAAAMAAAAAAAAAAAAAAAAAAAAAABnZW9nZWJyYS54bWxQSwUGAAAAAAEAAQA6AAAAcg0AAAAA" framePossible = "false" showResetIcon = "true" showAnimationButton = "true" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "true" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" allowRescaling = "true" />
| + | [[Didaktik der Bruchrechnung]]<br /> |
| − | |}
| + | |
| − | {|class="wikitable center"
| + | |
| − | |-
| + | |
| − | | colspan="2" style="background: #DDFFDD;"| <center>Objekt <math>\ G</math>, das in Klassen eingeteilt wird</center>
| + | |
| | | | |
| − | |-
| + | [[Allgemeiner Teil]]<br /> |
| − | | <math>\ G</math> ist eine ...
| + | |
| − | | <math>\ G</math> ist eine ...
| + | |
| | | | |
| − | |-
| + | [[Indoorcycling gegen Prüfungsangst]] |
| − | | colspan="2" style="background: #DDFFDD;"| <center>Dimension von <math>\ G</math></center>
| + | [[2013]] |
| | + | [[Quiz_Definition_1]] |
| | | | |
| − | |-
| + | [[Quiz_Definition_2]] |
| − | | Dimension von
| + | |
| − | | Dimension von
| + | |
| | | | |
| − | |-
| + | [[Quiz_Definition_3]] |
| − | | colspan="2" style="background: #DDFFDD;"| <center> Objekt <math>\ T</math>, das <math>\ G</math> in Klassen einteilt</center>
| + | |
| | | | |
| − | |-
| + | [[Ellipse]] |
| − | | <math>\ T</math> ist ...
| + | [[Schreibtest_mg]] |
| − | | <math>\ T</math> ist ...
| + | [[Sommersemester_2012]]<br /> |
| | + | [[Test]] <br /> |
| | + | [[Zwischenspeicher]] |
| | + | [[TKS]] |
| | + | [[Vorlage Aufgabe]] |
| | + | =Aufgaben zum Abstand= |
| | | | |
| − | |-
| + | ==Aufgabe 5.1== |
| − | | colspan="2" style="background: #DDFFDD;"| <center>Dimension von <math>\ T</math></center>
| + | <u>'''Satz:'''</u> |
| | + | ::Es seien <math>A,B</math> und <math>C</math> drei paarweise verschiedene Punkte.<br /> |
| | + | ::Wenn der Punkt <math>B</math> zwischen den Punkten <math>A</math> und <math>C</math> liegt, dann liegt weder <math>A</math> zwischen <math>B</math> und <math>C</math> noch <math>C</math> zwischen <math>A</math> und <math>B</math>. |
| | + | Beweisen Sie diesen Satz. |
| | | | |
| − | |-
| + | <br /> |
| − | | <math>\ T</math> hat die Dimension ...
| + | [[Lösung von Aufgabe 5.1_S (WS_12_13)]] |
| − | | <math>\ T</math> hat die Dimension ...
| + | |
| | | | |
| − | |-
| + | ==Aufgabe 5.2== |
| − | | colspan="2" style="background: #DDFFDD; "| <center>Referenzpunkt <math>\ Q</math> teilt <math>\ G \setminus_{\{ Q \}}</math> in genau zwei Klassen</center>
| + | Es seien <math>A</math>, <math>B</math>, <math>C</math> und <math>D</math> vier paarweise verschiedene Punkte. <br /> |
| | + | Beweisen Sie:<br /> |
| | + | <math>\overline{CD} \subset \overline{AB} \Rightarrow \forall P \in \overline{CD}: \operatorname{Zw}(APB}</math>. |
| | | | |
| − | |-
| |
| − | | colspan="2" |
| |
| − | <center>Klasse 1: </center>
| |
| − | <center>Menge aller Punkte <math>\ P\mathrm{\in }G</math> , die mit <math>\ Q</math> bezüglich <math>\ T</math> „auf derselben Seite liegen“</center>
| |
| | | | |
| − | |-
| |
| − | | <math>\ AQ^{+} = \{P| ... \}</math>
| |
| − | | <math>\ gQ^{+} = \{P| ... \}</math>
| |
| | | | |
| − | |-
| + | <br /><br /> |
| − | | colspan="2" |
| + | [[Lösung von Aufgabe 5.2_S (WS_12_13)]] |
| − | <center>Klasse 2:</center> | + | |
| − | <center>Menge aller Punkte <math>P\mathrm{\in }G</math>, die bezüglich <math>\ T</math> nicht auf der Seite von <math>\ Q</math>liegen.</center>
| + | |
| | | | |
| − | |-
| + | ==Aufgabe 5.3== |
| − | | <math>\ AQ^{-} = \{P| ... \}</math>
| + | Zeigen Sie, dass für drei paarweise verschiedene Punkte <math>\ A, B</math> und <math>\ C</math> gilt:<br /> |
| − | | <math>\ gQ^{-} = \{P| ... \}</math>
| + | Wenn <math> C \in \ AB^{+} </math> und <math>\left| AB \right| < \left| AC \right| </math> dann gilt <math>\operatorname Zw (A, B, C) </math> |
| | | | |
| − | |}
| + | <br /> |
| | + | [[Lösung von Aufgabe 5.3_S (WS_12_13)]] |
| | | | |
| − | === Definition des Begriffs der Halbebene ===
| |
| − | ==== Alles hat zwei Seiten oder grundlegende Ideen der Beschaffenheit von Ebenen ====
| |
| − | {|
| |
| − | |-
| |
| − | | Zu unsere Vorstellung von der Eigenschaften einer beliebigen Ebene <math>\Epsilon</math> gehört u.a., dass jede Gerade <math>\ g</math>, die zu unserer jeweiligen Ebene <math>\Epsilon</math> gehört, diese in zwei ''Hälften'' bzw. zwei ''Seiten'' einteilt. Zur Kennzeichnung der beiden ''Seiten'' von <math>\Epsilon</math> bezüglich der Geraden <math>\ g</math> verwenden wir einen Punkt <math>\ Q \in \Epsilon</math>, welcher nicht zu <math>\ g</math> gehören sollte.
| |
| − | |[[Bild:Halbebene_00.png| 100 px]]
| |
| − | |-
| |
| − | | Zu der einen ''Hälfte'' von <math>\ \Epsilon</math> bezüglich <math>\ g</math> gehören alle die Punkte aus <math>\Epsilon \setminus g</math>, die mit <math>\ Q</math> auf derselben Seite von <math>\ g</math> liegen. Alle anderen Punkte aus <math>\Epsilon \setminus g</math> gehören zur anderen Seite von <math>\ \Epsilon</math> bezüglich <math>\ g</math>.
| |
| − | | [[Bild:Halbebene_01.png | 100 px]]
| |
| − | |}
| |
| − | ==== Offene Halbebenen ====
| |
| − | Die beiden Seiten, in die die Menge der Punkte einer Ebene <math>\ \Epsilon</math>, die nicht auf einer Geraden <math>\ g</math> dieser Ebene liegen, durch diese Gerade <math>\ g</math> eingeteilt wird, heißen offene Halbebenen von <math>\ \Epsilon</math> bezüglich der Trägergeraden <math>\ g</math>. Der nicht zu <math>\ g</math> gehörende Referenzpunkt <math>\ Q \in \Epsilon</math> bietet uns eine Möglichkeit zur Bezeichnung der beiden offenen Halbebenen. Die offene Halbebene, zu der alle Punkte gehören, die bezüglich <math>\ g</math> mit <math>\ Q</math> auf derselben Seite liegen, wird mit <math>\ gQ^{+}</math> bezeichnet, die andere offene Halbebene von <math>\ \Epsilon</math> bezüglich <math>\ g</math> und <math>\ Q</math> mit <math>\ gQ^{-}</math>.
| |
| | | | |
| − | Obige Ausführungen können als informelle Definition des Begriffs offene Halbebene dienen. Hinsichtlich der wirklicher mathematischer Exaktheit bezüglich der Festlegung, was denn eine offene Halbene sein möge bedarf es einer genauereren Erklärung, was es denn darunter zu verstehen wäre, dass zwei Punkte <math>\ P</math> und <math> \ Q</math> einer Ebene <math>\ \Epsilon</math> auf ein und derselben bzw. auf zwei verschiedenen Seiten dieser Ebene bezüglich einer Geraden <math>\ g</math> liegen.
| + | ==Aufgabe 5.4== |
| | + | Beweisen Sie: Zu jeder Strecke <math>\overline{AB} </math> existiert genau eine Strecke <math>\overline{AC} </math> auf <math>\ AB^{+} </math> mit <math>\left| AB \right| = \frac{1}{4} \left| AC \right| </math> und <math>\overline{AB} </math> <math> \subset</math> <math>\overline{AC} </math> |
| | + | <br /> |
| | + | |
| | + | <br /><br /> |
| | + | [[Lösung von Aufgabe 5.4_S (WS_12_13)]] |
| | + | |
| | + | =Weitere Aufgabe zur Inzidenz= |
| | + | |
| | + | |
| | + | == Aufgabe 5.5 == |
| | + | Beweisen Sie: Je vier nicht komplanare Punkte sind paarweise verschieden (Hinweis: Nutzen Sie bei der Beweisführung die Sätze aus Aufgabe 4.3 und Zusatzaufgabe 4.4).<br /><br /> |
| | + | [[Lösung von Aufg. 5.5_S (WS_12_13)]]<br /> |
| | + | <br /> |
Beweisen Sie diesen Satz.
Beweisen Sie: Je vier nicht komplanare Punkte sind paarweise verschieden (Hinweis: Nutzen Sie bei der Beweisführung die Sätze aus Aufgabe 4.3 und Zusatzaufgabe 4.4).
Lösung von Aufg. 5.5_S (WS_12_13)
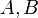 und
und  drei paarweise verschiedene Punkte.
drei paarweise verschiedene Punkte. zwischen den Punkten
zwischen den Punkten  und
und  liegt, dann liegt weder
liegt, dann liegt weder  zwischen
zwischen  und
und  noch
noch  zwischen
zwischen  und
und  .
.
 ,
,  ,
,  und
und  vier paarweise verschiedene Punkte.
vier paarweise verschiedene Punkte.  und
und  gilt:
gilt: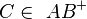 und
und 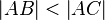 dann gilt
dann gilt 
 existiert genau eine Strecke
existiert genau eine Strecke  auf
auf  mit
mit 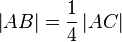 und
und 



