Lösung von Aufg. 11.7 (WS 11/12): Unterschied zwischen den Versionen

Version vom 4. Januar 2012, 13:00 Uhr

Beweisen Sie die Gültigkeit der Umkehrung des Basiswinkelsatzes

Vorr.: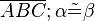 $\overline{ABC} ; \alpha \tilde {=} \beta$

Beh.: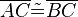 $\overline{AC} \tilde {=} \overline{BC}$

Beweis:

Schritt	Begründung
(1)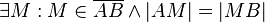 $\exists M:M\in \overline{AB} \wedge \left\| AM \right\| =\left\| MB \right\|$	Existenz und Eindeutigkeit des Mittelpunktes
(2) 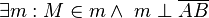$\exists m:M\in m \wedge \ m \perp \overline{AB}$	Existenz und Eindeutigkeit der Mittelsenkrechten, (1)
(3) zu Zeigen: 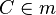$C\in m$	Dann gilt die Behauptung, Satz. Jeder Punkt vom m hat den selben Abstand zu A und B
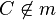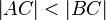(4) Ann.: $C\not\in m$ d.h. o.B.d.A. $\left\| AC \right\| < \left\| BC \right\|$
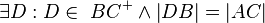(5) $\exists D: D\in \ BC^{+} \wedge \left\| DB \right\| = \left\| AC \right\|$	Axiom vom Lineal, Abstandsaxiom, (4)
(6) C im inneren von 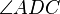$\angle ADC$	Winkeladditonsaxiom (5)
(7) 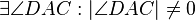$\exists \angle DAC : \|\angle DAC\| \neq 0$	(4),(5),(6)
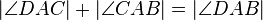(8) $\|\angle DAC\| + \|\angle CAB\| = \|\angle DAB\|$	(5),(6),(7) Winkeladditonsaxiom
(9) 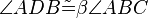$\angle ADB \tilde {=} \beta \angle ABC$	Basiswinkelsatz (5)
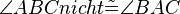(10) $\angle ABC nicht \tilde {=} \angle BAC$ Wiederspruch zur Vorr., Annahme verwerfen, Behaupt stimmt	(9),(8),(7),(5)

--RicRic 13:04, 3. Jan. 2012 (CET)

@@ Zeile 25: / Zeile 25: @@
 |  (7) <math>\exists \angle DAC : |\angle DAC| \neq 0</math> || (4),(5),(6)
 |-
-|  (8) <math>|\angle DAC| + |\angle ABC|  = |\angle DAB|</math>  || (5),(6),(7) Winkeladditonsaxiom
+|  (8) <math>|\angle DAC| + |\angle CAB|  = |\angle DAB|</math>  || (5),(6),(7) Winkeladditonsaxiom
 |-
 |  (9) <math>\angle ADB \tilde {=} \beta   \angle ABC</math>  || Basiswinkelsatz (5)