Übung Aufgaben 10 (SoSe 12)

Aufgabe 10.1

Definieren Sie den Begriff "Gleichschenkliges Dreieck". Bringen Sie in der Definition die Begriffe Basis, Basiswinkel und Schenkel eines gleichschenkligen Dreiecks unter.
Lösung von Aufgabe 10.1P (SoSe_12)

Aufgabe 10.2

Formulieren Sie die Umkehrung des Basiswinkelsatzes.
Lösung von Aufgabe 10.2P (SoSe_12)

Aufgabe 10.3

Beweisen Sie mit abbildungsgeometrischen Mitteln die Umkehrung des Basiswinkelsatzes.
Lösung von Aufgabe 10.3P (SoSe_12)

Aufgabe 10.4

Beweisen Sie Satz IX.3: Bei einer Punktspiegelung ist der Schnittpunkt S der beiden Spiegelgeraden a und b Mittelpunkt der Strecke 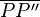$\overline{PP''}$, mit $P''=a\circ b(P)$.
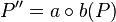Lösung von Aufgabe 10.4P (SoSe_12)

Aufgabe 10.5

Beweisen Sie Satz IX.4: Bei einer Punktspiegelung werden Geraden stets auf parallele Bildgeraden abgebildet.
Lösung von Aufgabe 10.5P (SoSe_12)

Aufgabe 10.6

1. Gegeben sei ein Winkel $\angle ABC$ und ein Punkt P im Inneren des Winkels der nicht auf einem der Schenkel des Winkels $\angle ABC$ liegt. Konstruieren Sie eine Strecke $\overline{DE}$ deren Endpunkte D und E jeweils auf einem der beiden Schenkel des Winkels $\angle ABC$ liegen und P Mittelpunkt der Strecke $\overline{DE}$ ist.
2. Beweisen Sie, dass Ihre Konstruktion richtig ist.

Lösung von Aufgabe 10.6P (SoSe_12)