Übung Aufgaben 11 (SoSe 13)
Inhaltsverzeichnis |
Aufgabe 11.1
Das Rechteck  soll durch eine Drehung auf das blaue Rechteck abgebildet werden. Konstruieren Sie den Drehpunkt. Wo müssen die beiden Achsen liegen, wenn die Drehung durch eine Verkettung zweier Achsenspiegelungen erzeugt werden soll?
soll durch eine Drehung auf das blaue Rechteck abgebildet werden. Konstruieren Sie den Drehpunkt. Wo müssen die beiden Achsen liegen, wenn die Drehung durch eine Verkettung zweier Achsenspiegelungen erzeugt werden soll?
Lösung von Aufgabe 11.1P (SoSe_13)
Aufgabe 11.2
Beweisen Sie die Umkehrung des Wechselwinkelsatzes mit abbildungsgeometrischen Methoden. Hinweis: Der Wechselwinkelsatz ist bereits bewiesen.
Lösung von Aufgabe 11.2P (SoSe_13)
Aufgabe 11.3
Beweisen Sie: Bei Spiegelungen, Stöße beim Billard über Bande, etc. gilt stets: Einfallswinkel  gleich Ausfallswinkel
gleich Ausfallswinkel  (siehe GeoGebra-Applet).
(siehe GeoGebra-Applet).
Lösung von Aufgabe 11.3P (SoSe_13)
Aufgabe 11.4
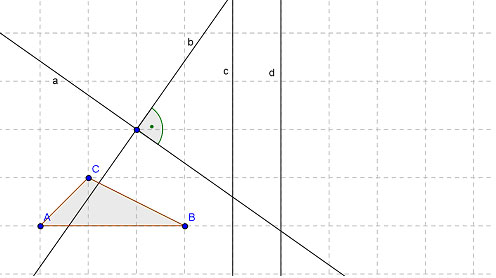
Gegeben sei ein Dreieck  und die Geraden a, b, c und d mit:
und die Geraden a, b, c und d mit: 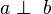 und
und 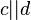 entsprechend der Skizze.
entsprechend der Skizze.
- Durch welche Abbildung kann die Verkettung der vier Geradenspiegelungen
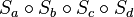 ersetzt werden (Begründen Sie Ihre Entscheidung)?
ersetzt werden (Begründen Sie Ihre Entscheidung)?
- Zeichnen Sie die Achsen der Ersatzabbildung in die Skizze oben ein. Hinweis: Sie dürfen das Gitter im Hintergrund als Orientierung nutzen.
- Konstruieren Sie oben in der Skizze das Bild des Dreiecks
 , das nach der Verkettung
, das nach der Verkettung 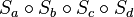 entsteht, mit Hilfe der Ersatzabbildung.
entsteht, mit Hilfe der Ersatzabbildung.
Lösung von Aufgabe 11.4P (SoSe_13)
Aufgabe 11.5
Zeigen Sie, dass die Verkettung einer Drehung 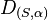 mit einer Verschiebung wieder eine Drehung
mit einer Verschiebung wieder eine Drehung 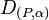 ergibt. Wo liegt das neue Drehzentrum P?
ergibt. Wo liegt das neue Drehzentrum P?
Lösung von Aufgabe 11.5P (SoSe_13)