Das Wiki für die Lehrveranstaltung Lineare Algebra/analytische Geometrie SoSe 2020
|
Das Wiki für die Lehrveranstaltung "Lineare Algebra/analytische Geometrie", Sommersemester 2020Literatur und mehr
Aus früheren Semestern
Sommersemester 2020Prüfungsthemen und KontrollfragenPrüfungsthemen und Kontrollfragen SoSe 2020 ÜbungsaufgabenDie Lehrveranstaltung Lineare Algebra/analytische Geometrie im CoronasemesterUngewöhnliche Umstände erfordern ungewöhnliche Maßnahmen. Aus diesem Grunde versuche ich mich als Lehrender an einer Methode, die ich bislang vehement ablehnte: Der Flipped Classroom. Flipped Classroom bedeutet eigentlich, dass Sie vorab im Selbststudium sich den Lehrstoff aneignen, um ihn dann in einer Präsenzveranstaltung zu vertiefen. Aus Gründen unserer aller gesundheitlichen Unversehrtheit wird die Präsenzveranstaltung allerdings nicht als solche, sondern virtuell mit Hilfe eines Videokonferenzsystems stattfinden. Die PH hat entsprechende Lizenzen der Software Zoom gekauft. Die virtuellen Konferenzen finden jeweils zu den ursprünglich geplanten Terminen der entsprechenden Vorlesung statt. Im Fall der Linearen Algebra also jeden Freitag von 12 bis 14 Uhr. Zur Teilnahme an den Videokonferenzen erhalten Sie per Mail einen Link. Diesbezüglich müssen Sie sich zur Lehrveranstaltung in StudIp angemeldet haben. Zur Vorbereitung auf die virtuellen Konferenzen erhalten Sie hier im Wiki jeweils entsprechende Materialien und Übungsaufgaben. Damit wir ähnliche Bedingungen wie bei einer Übung in der PH haben, werden wir zusätzlich zu Zoom die Software Whiteboard von Microsoft nutzen. Whiteboard erlaubt es, jedem Teilnehmer Notizen, Skizzen und Bemerkungen in ein gemeinsames Dokument zu schreiben. Die Bedienung von Whiteboard erfolgt sinnvollerweise mit einem Stift oder dem Finger, d.h. ein Touchscreen ist für Whiteboard sinnvoll. Ferner werden wir das dynamische Geometriesystem Geogebra nutzen.
Links zu den einzelnen LehrveranstaltungenMeeting vom 24. April 2020Meeting vom 08. Mai 2020Meeting vom 15. Mai 2020Meeting vom 22. Mai 2020Übung vom 5. Juni 2020Meeting vom 26. Juni 2020Meeting vom 03.Juli 2020Ziele und Klassifizierung des Lehrstoffs der Lehrveranstaltung LinAlg/anaGeoZiel der Lehrveranstaltung ist es, die Teilnehmerinnen und Teilnehmer aus fachlicher Sicht zu befähigen, folgende Inhalte des Mathematikunterrichts der Sekundarstufe I fundiert zu unterrichten:
Hierzu wird das schulische mathematische Wissen und Können der Teilnehmerinnen und Teilnehmer (inklusive der Abiturkurses) reaktiviert, umstrukturiert und in größere Zusammenhänge und Konzepte integriert. Eine Ausrichtung der Inhalte an denen einer üblichen Lehrveranstaltung zur linearen Algebra etwa an Universitäten wird nicht angestrebt. Konkret heißt das, dass die lineare Algebra hier nicht im Rahmen einer Theorie mehr oder weniger abstrakter reeller Vektorräume unterrichtet wird. Vektoren werden lediglich mehr oder weniger anschaulich als Pfeilklassen und zugehörige geordnete Paare bzw. Tripel reeller Zahlen verwendet. Der Lehrstoff wird in der folgenden Abfolge mit folgenden Inhalten gefüllt werden: Wiederholung und Vertiefung grundlegenden SchulwissensKreise und Sinus und Kosinus am Einheitskreis
Parallelogramme
Strahlensätze und Ähnlichkeit
Pfeilklassen
Das Skalarprodukt
Proportionalität und Geradengleichungen in der Schule
Lineare Gleichungssysteme mit zwei Gleichungen und zwei UnbekanntenDie Geradengleichung ax+by+c=0
Lineare Gleichungssysteme mit zwei Gleichungen und zwei Unbekannten als Schnittpunktberechnung zweier Geraden
Lineare Gleichungssysteme mit zwei Gleichungen und zwei Unbekannten in Matrixform
Lineare Gleichungssysteme mit drei Gleichungen und drei UnbekanntenDie Ebenengleichung ax+by+cz+d=0
Geraden im Raum
Lösen von lineare Gleichungssysteme mit drei Gleichungen und drei Unbekannten
|
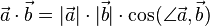
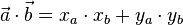
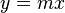
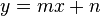
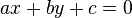 und umgekehrt.
und umgekehrt.
 und
und  als Komponenten eines Normalenvektors bzgl. der durch die Gleichung beschriebenen Geraden.
als Komponenten eines Normalenvektors bzgl. der durch die Gleichung beschriebenen Geraden.
 als Skalarprodukt
als Skalarprodukt
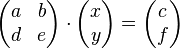
 als Normalenvektor zur Ebene
als Normalenvektor zur Ebene 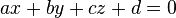
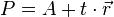
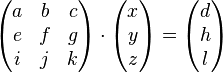 kleine Koeffizientenmatrix, große Koeffizientenmatrix
kleine Koeffizientenmatrix, große Koeffizientenmatrix

