Übung Aufgaben 11 (WS 11/12): Unterschied zwischen den Versionen
(Die Seite wurde neu angelegt: „== Aufgabe 11.1 == Warum ist die folgende Definition des Begriffs ''Winkelhalbierende'' nicht korrekt? Die Halbgerade <math>\ SW^+</math> ist die Winkelhalbieren…“) |
(→Aufgabe 11.5) |
||
| Zeile 28: | Zeile 28: | ||
==Aufgabe 11.5 == | ==Aufgabe 11.5 == | ||
| − | Formulieren Sie den Basiswinkelsatz ([[ | + | Formulieren Sie den Basiswinkelsatz ([[Basiswinkelsatz_und_Mittelsenkrechtenkriterium_WS_11/12#Satz_VII.5:_Basiswinkelsatz|Satz VII.5]]) auf zwei weitere Arten und Weisen. |
[[Lösung von Aufg. 11.5 (WS_11/12)]] | [[Lösung von Aufg. 11.5 (WS_11/12)]] | ||
Aktuelle Version vom 1. Januar 2012, 19:09 Uhr
Inhaltsverzeichnis |
Aufgabe 11.1
Warum ist die folgende Definition des Begriffs Winkelhalbierende nicht korrekt?
Die Halbgerade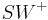 
ist die Winkelhalbierende des Winkels 
, wenn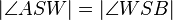 
.
Eine Skizze genügt.
Lösung von Aufg. 11.1 (WS_11/12)
Aufgabe 11.2
Beweisen Sie Satz VI.eineinhalb
Lösung von Aufg. 11.2 (WS_11/12)
Aufgabe 11.3
Beweisen Sie: Zu jedem Winkel gibt es genau eine Winkelhalbierende.
Lösung von Aufg. 11.3 (WS_11/12)
Aufgabe 11.4
Definieren Sie den Begriff des gleichschenkligen Dreiecks. Bringen Sie in der Definition die Begriffe Basis, Basiswinkel und Schenkel eines gleichschenkligen Dreiecks unter.
Hinweis: Die Schenkel eine Winkels sind Strahlen. Die Schenkel eines gleichschenkligen Dreiecks sind Strecken.
Lösung von Aufg. 11.4 (WS_11/12)
Aufgabe 11.5
Formulieren Sie den Basiswinkelsatz (Satz VII.5) auf zwei weitere Arten und Weisen.
Lösung von Aufg. 11.5 (WS_11/12)
Aufgabe 11.6
Formulieren Sie die Umkehrung des Basiswinkelsatzes
Lösung von Aufg. 11.6 (WS_11/12)
Aufgabe 11.7
Beweisen Sie die Gültigkeit der Umkehrung des Basiswinkelsatzes
