Serie 12 SoSe 2013: Unterschied zwischen den Versionen
*m.g.* (Diskussion | Beiträge) (→Aufgabe 12.08) |
*m.g.* (Diskussion | Beiträge) (→Aufgabe 12.10) |
||
| (3 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt) | |||
| Zeile 47: | Zeile 47: | ||
==Aufgabe 12.09 == | ==Aufgabe 12.09 == | ||
| + | Informieren Sie sich, was Peripheriewinkel (Umfangswinkel) und Zentriwinkel (Mittelpunktswinkel) sind und definieren Sie diese Begriffe. | ||
<br /> | <br /> | ||
[[Lösung von Aufgabe 12.09_SoSe_13]] | [[Lösung von Aufgabe 12.09_SoSe_13]] | ||
==Aufgabe 12.10== | ==Aufgabe 12.10== | ||
| − | + | Formulieren Sie den Satz des Thales in Wenn-Dann-Form und beweisen sie ihn.<br /> | |
| + | [[Lösung von Aufgabe 12.10_SoSe_13]] | ||
<!--- Was hier drunter steht muss stehen bleiben ---> | <!--- Was hier drunter steht muss stehen bleiben ---> | ||
Aktuelle Version vom 18. Juli 2013, 22:09 Uhr
Aufgabe 12.01Mark definiert: Es sei Aufgabe 12.02Definieren Sie die Begriffe Kreistangente, Berührungspunkt einer Kreistangente und Berührungsradius einer Kreistangente.
Aufgabe 12.03Alles in ein und derselben Ebene: Aufgabe 12.04Die Gerade Lösung von Aufg. 12.04_SoSe_13 Aufgabe 12.05Definieren Sie den Begriff Inkreis eines Dreiecks unter der Verwendung des Begriffs Tangente.
Aufgabe 12.06Beweisen Sie: Die Winkelhalbierenden eines Dreiecks Lösung von Aufg. 12.06_SoSe_13 Aufgabe 12.07Definieren Sie den Begriff der Höhen eines Dreiecks.
Aufgabe 12.08Beweisen Sie: Die Höhen eines Dreiecks schneiden sich in genau einem Punkt. Das folgende Applet hilft: Hinweis: Ein Klick auf den Button Rechts unten liefert die Konstruktionsbeschreibung. Lösung von Aufgabe 12.08_SoSe_13 Aufgabe 12.09Informieren Sie sich, was Peripheriewinkel (Umfangswinkel) und Zentriwinkel (Mittelpunktswinkel) sind und definieren Sie diese Begriffe.
Aufgabe 12.10Formulieren Sie den Satz des Thales in Wenn-Dann-Form und beweisen sie ihn. |
 ein rechtwinkliges Dreieck. Die längste Seite von
ein rechtwinkliges Dreieck. Die längste Seite von  ein Kreis mit dem Mittelpunkt
ein Kreis mit dem Mittelpunkt  . Ferner seien
. Ferner seien  ein Punkt von
ein Punkt von  eine Gerade durch
eine Gerade durch  steht. Beweisen Sie:
steht. Beweisen Sie: 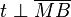 .
.
 , welcher der Mittelpunkt des Inkreises von
, welcher der Mittelpunkt des Inkreises von 
