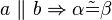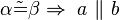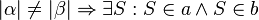Übung Aufgaben 4 (WS 16 17): Unterschied zwischen den Versionen
(Die Seite wurde neu angelegt: „=Aufgaben zu Sätzen und Beweisen= ==Aufgabe 4.1== Der Basiswinkelsatz lautet: Im gleichschenkligen Dreieck sind die Basiswinkel kongruent zueinander.<br /> a)…“) |
AlanTu (Diskussion | Beiträge) K |
||
| Zeile 8: | Zeile 8: | ||
==Aufgabe 4.2== | ==Aufgabe 4.2== | ||
| − | + | {{WS2016-2017/MAT01/Mathematische Grundlagen Ⅱ: Geometrie/Woche 4/Aufgabe 2}} | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
[[Lösung von Aufgabe 4.2 (WS_16/17)]] | [[Lösung von Aufgabe 4.2 (WS_16/17)]] | ||
| Zeile 52: | Zeile 37: | ||
| − | + | {{WS2016-2017/MAT01/Mathematische Grundlagen Ⅱ: Geometrie/Navigationsleiste Aufgaben}} | |
| − | [[ | + | [[Kategorie:Übung 4 (Wintersemester 2016/2017)]] |
| + | [[Kategorie:Aufgaben (Wintersemester 2016/2017)]] | ||
Aktuelle Version vom 9. November 2016, 20:40 Uhr
Inhaltsverzeichnis |
Aufgaben zu Sätzen und Beweisen
Aufgabe 4.1
Der Basiswinkelsatz lautet: Im gleichschenkligen Dreieck sind die Basiswinkel kongruent zueinander.
a) Wie lautet die Umkehrung des Basiswinkelsatzes?
b) Fassen Sie den Basiswinkelsatz und seine Umkehrung zu einem Satz zusammen.
Lösung von Aufgabe 4.1 (WS_16/17)
Aufgabe 4.2
Satz: In einem Dreieck 
mit 
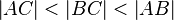sind die Winkel 
und 
nicht kongruent zueinander.
a) Welcher Beweis ist korrekt?
Begründen Sie ausführlich! (Der Basiswinkelsatz und seine Umkehrung seien bereits bewiesen.)
Beweis 1
Sei ein Dreieck.
- Voraussetzung
- .
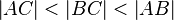- Behauptung
-
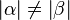
- Beweis
-
Da nach Voraussetzung
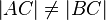gilt, folgt nach dem Basiswinkelsatz 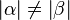.Damit ist der Satz bewiesen.
Beweis 2
Sei ein Dreieck.
- Voraussetzung
- .
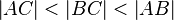- Behauptung
-
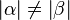
- Beweis
-
Nach Umkehrung des Basiswinkelsatzes gilt: Wenn
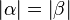dann gilt 
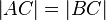.Die Kontraposition der Umkehrung lautet also: Wenn
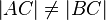dann gilt 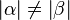.Da die Kontraposition gleichwertig ist, kann man auch diese beweisen.
Da nach Voraussetzung gilt:
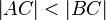, d.h. 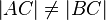, kann nach Kontraposition der Umkehrung des Basiswinkelsatzes direkt gefolgert werden: 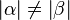.Damit ist der Satz bewiesen.
b) Beweisen Sie den Satz indirekt mit Widerspruch
Lösung von Aufgabe 4.2 (WS_16/17)
Aufgabe 4.3
a) Wie lautet der Stufenwinkelsatz? (schauen Sie bei Bedarf in Schulbüchern nach).
b) Es seien a und b zwei nichtidentische Geraden, die durch eine dritte Gerade c jeweils in genau einem Punkt geschnitten werden. Bei diesem Schnitt entstehen die Stufenwinkel und . Welche der folgenden Aussagen repräsentiert den Stufenwinkelsatz bzw. ist eine zu diesem Satz äuivalente Aussage (Begründen Sie jeweils)?
Lösung von Aufgabe 4.3 (WS_16/17)
Aufgabe 4.4
Wir gehen von folgender Implikation aus: Wenn zwei Geraden g und h nicht identisch sind, dann haben sie höchstens einen Punkt gemeinsam.
a) Wie lautet die Kontraposition dieser Implikation?
b) Wie lautet die Annahme, wenn Sie diese Implikation durch einen Widerspruch beweisen möchten?
Lösung von Aufgabe 4.4 (WS_16/17)
Aufgabe 4.5
Vergleichen Sie die Wahrheitswerte von
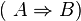und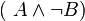 
.
Erklären Sie den Zusammenhang zwischen Ihrer Wahrheitstabelle und dem indirekten Beweis durch Widerspruch.
Lösung von Aufgabe 4.5 (WS_16/17)
