Übung Aufgaben 13 (WS 11/12): Unterschied zwischen den Versionen
(Die Seite wurde neu angelegt: „== Aufgabe 13.1 == 1. Es sei <math>\overline{ABC}</math> ein Dreieck mit den schulüblichen Bezeichnungen. Beweisen Sie Satz IX.3:<math>\left| \alpha \right| \ …“) |
|||
| Zeile 1: | Zeile 1: | ||
== Aufgabe 13.1 == | == Aufgabe 13.1 == | ||
| − | + | Es sei <math>\overline{ABC}</math> ein Dreieck mit den schulüblichen Bezeichnungen. | |
Beweisen Sie Satz IX.3:<math>\left| \alpha \right| \ >\left| \beta \right|\Rightarrow \left| a \right| \ >\left| b \right|</math> | Beweisen Sie Satz IX.3:<math>\left| \alpha \right| \ >\left| \beta \right|\Rightarrow \left| a \right| \ >\left| b \right|</math> | ||
Aktuelle Version vom 19. Januar 2012, 11:43 Uhr
Inhaltsverzeichnis[Verbergen] |
Aufgabe 13.1
Es sei 
ein Dreieck mit den schulüblichen Bezeichnungen.
Beweisen Sie Satz IX.3:
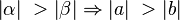
Lösung von Aufg. 13.1 (WS_11/12)
Aufgabe 13.2
Beweisen Sie: Wenn 
ein Punkt außerhalb der Geraden 
ist, dann gibt es eine Gerade 
, die durch geht und parellel zu ist.
Lösung von Aufg. 13.2 (WS_11/12)
Aufgabe 13.3
Gegen welche Forderung, die an Axiomensysteme zu stellen ist, verstößt die folgende Formulierung des Parallelenaxioms:
Zu jedem Punkt außerhalb einer Geraden gibt es genau eine Gerade , die durch geht und zu parallel ist.
Lösung von Aufg. 13.3 (WS_11/12)
Aufgabe 13.4
Definieren Sie die Begriffe Stufenwinkel, Wechselwinkel und entgegengesetzt liegende Winkel.
Lösung von Aufg. 13.4 (WS_11/12)
Aufgabe 13.5
Beweisen Sie den Stufenwinkelsatz.
Lösung von Aufg. 13.5 (WS_11/12)
Aufgabe 13.6
Beweisen Sie den Innenwinkelsatz für Dreiecke.
Lösung von Aufg. 13.6 (WS_11/12)
Aufgabe 13.7
Beweisen Sie: Ein Punkt gehört genau dann zur Winkelhalbierenden des Winkels 
, wenn er zu den Schenkeln von jeweils denselben Abstand hat.
