Übung Aufgaben 10 (SoSe 13)
Inhaltsverzeichnis |
Aufgabe 10.1
Definieren Sie den Begriff "Gleichschenkliges Dreieck". Bringen Sie in der Definition die Begriffe Basis, Basiswinkel und Schenkel eines gleichschenkligen Dreiecks unter.
Lösung von Aufgabe 10.1P (SoSe_13)
Aufgabe 10.2
Beweisen Sie mit abbildungsgeometrischen Mitteln den Basiswinkelsatz.
Lösung von Aufgabe 10.2P (SoSe_13)
Aufgabe 10.3
Welche wichtige Erkenntnis ergibt sich aus Satz IX.2 für die absolute und relative Lage der beiden Spiegelgeraden? Nutzen Sie diese Erkenntnis für die Lösung der folgenden beiden Aufgaben.
Zu Satz IX.2: http://wikis.zum.de/geowiki/Verkettung_zweier_Geradenspiegelungen_WS_12_13#Satz_IX.2_:
Lösung von Aufgabe 10.3P (SoSe_13)
Aufgabe 10.4
Beweisen Sie Satz IX.3:
Bei einer Punktspiegelung ist der Schnittpunkt S der beiden Spiegelgeraden a und b Mittelpunkt der Strecke 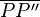 , mit
, mit 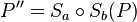 .
.
Lösung von Aufgabe 10.4P (SoSe_13)
Aufgabe 10.5
Beweisen Sie Satz IX.4:
Bei einer Punktspiegelung werden Geraden stets auf parallele Bildgeraden abgebildet.
Lösung von Aufgabe 10.5P (SoSe_13)

